Skip to article frontmatterSkip to article content
import numpy as np
import pandas as pd
import torch
from torch import nn, optim
import statsmodels.api as sm
import matplotlib.pyplot as plt
from statsmodels.tsa.arima.model import ARIMA

Model Fitting using PyTorch

We will fit some basic nonlinear models using PyTorch. Let us start with the change of slope model that we already studied in Lecture 9.

Change of Slope Model (from Lecture 9)

The model is:

yt=β0+β1t+β2ReLU(t−c1)+β3ReLU(t−c2)+ϵty_t = \beta_0 + \beta_1 t + \beta_2 \text{ReLU}(t - c_1) + \beta_3 \text{ReLU}(t - c_2) + \epsilon_t

We shall write xt=tx_t = t so that the model becomes

yt=β0+β1xt+β2ReLU(xt−c1)+β3ReLU(xt−c2)+ϵty_t = \beta_0 + \beta_1 x_t + \beta_2 \text{ReLU}(x_t - c_1) + \beta_3 \text{ReLU}(x_t - c_2) + \epsilon_t

Our older code (in Lecture 9) involved calculating RSS(c1,c2)RSS(c_1, c_2) and then optimizing over c1c_1 and c2c_2 using a grid. Today, we shall fit this model using a PyTorch neural network.

TTLCONS Dataset

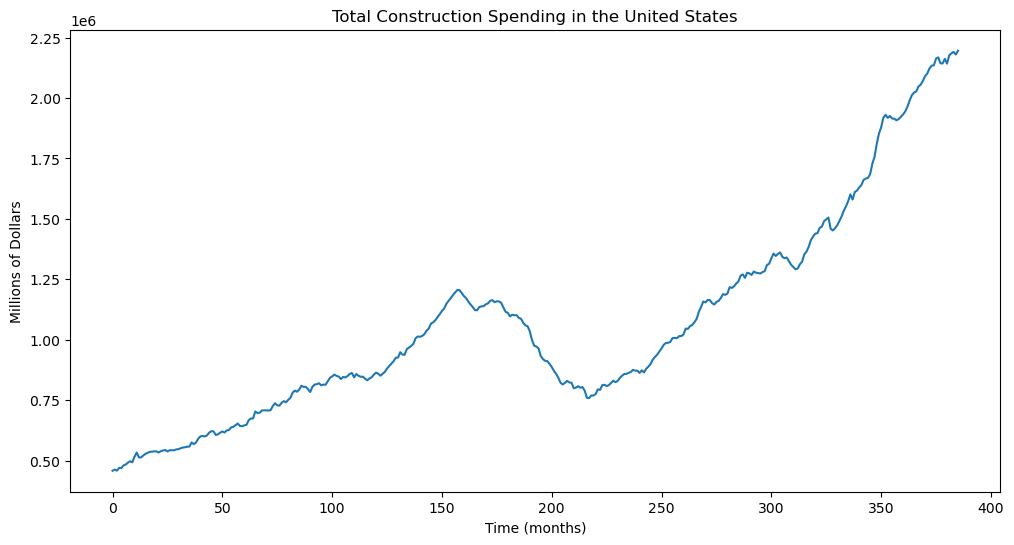
Let us apply the change of slope model to the TTLCONS dataset.

ttlcons = pd.read_csv('TTLCONS_14April2025.csv')
print(ttlcons.head(10))
print(ttlcons.tail(10))
y_raw = ttlcons['TTLCONS']
n = len(y_raw)
x_raw = np.arange(1, n+1)
plt.figure(figsize = (12, 6))
plt.plot(y_raw)
plt.xlabel("Time (months)")
plt.ylabel('Millions of Dollars')
plt.title("Total Construction Spending in the United States")
plt.show()
  observation_date  TTLCONS
0       1993-01-01   458080
1       1993-02-01   462967
2       1993-03-01   458399
3       1993-04-01   469425
4       1993-05-01   468998
5       1993-06-01   480247
6       1993-07-01   483571
7       1993-08-01   491494
8       1993-09-01   497297
9       1993-10-01   492823
    observation_date  TTLCONS
376       2024-05-01  2168211
377       2024-06-01  2143970
378       2024-07-01  2143139
379       2024-08-01  2162132
380       2024-09-01  2142427
381       2024-10-01  2176627
382       2024-11-01  2184796
383       2024-12-01  2191059
384       2025-01-01  2179942
385       2025-02-01  2195755
<Figure size 1200x600 with 1 Axes>

Here is the code we used in Lecture 9 for fitting this model.

#Older code that we used to fit this model: 
def rss(c):
    n = len(y_raw)
    x_raw = np.arange(1, n+1)
    X = np.column_stack([np.ones(n), x_raw])
    if np.isscalar(c):
        c = [c]
    for j in range(len(c)):
        xc = ((x_raw > c[j]).astype(float))*(x_raw-c[j])
        X = np.column_stack([X, xc])
    md = sm.OLS(y_raw, X).fit()
    ans = np.sum(md.resid ** 2)
    return ans

c1_gr = np.arange(1, n-1)
c2_gr = np.arange(1, n-1)
X, Y = np.meshgrid(c1_gr, c2_gr)
g = pd.DataFrame({'x': X.flatten(), 'y': Y.flatten()})
g['rss'] = g.apply(lambda row: rss([row['x'], row['y']]), axis = 1)

min_row = g.loc[g['rss'].idxmin()]
print(min_row)
c_opt = min_row[:-1]
print(c_opt)
x      2.250000e+02
y      1.750000e+02
rss    1.368859e+12
Name: 67040, dtype: float64
x    225.0
y    175.0
Name: 67040, dtype: float64

c = np.array(c_opt)
n = len(y_raw)
x_raw = np.arange(1, n+1)
X = np.column_stack([np.ones(n), x_raw])
if np.isscalar(c):
    c = np.array([c])
for j in range(len(c)):
    xc = ((x_raw > c[j]).astype(float))*(x_raw-c[j])
    X = np.column_stack([X, xc])
md_c2 = sm.OLS(y_raw, X).fit()
print(md_c2.summary())
rss_copt = (np.sum((md_c2.resid ** 2)))/n
print(rss_copt) #this is the smallest value of the loss achieved. 
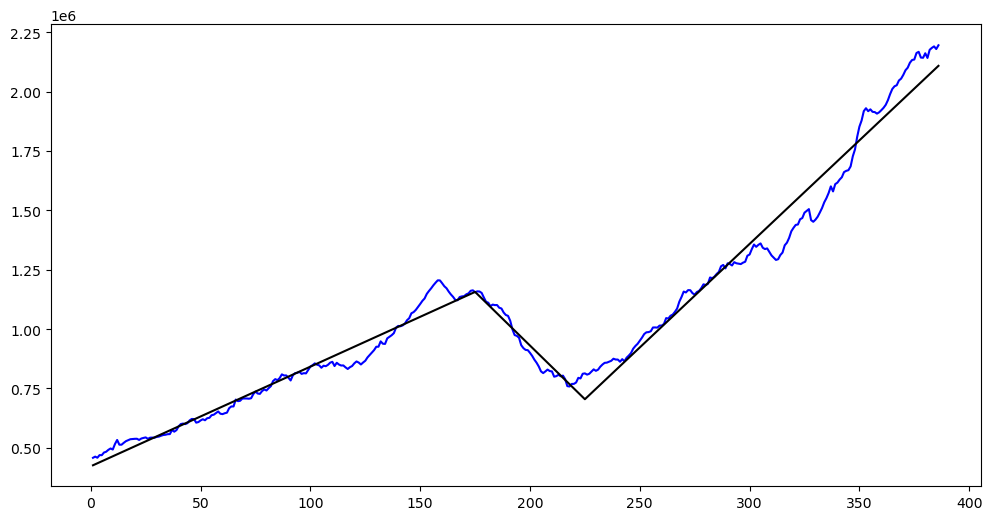
plt.figure(figsize = (12, 6))
plt.plot(tme, y_raw, color = 'blue')
plt.plot(tme, md_c2.fittedvalues, color = 'black')
plt.show()
                            OLS Regression Results                            
==============================================================================
Dep. Variable:                TTLCONS   R-squared:                       0.980
Model:                            OLS   Adj. R-squared:                  0.980
Method:                 Least Squares   F-statistic:                     6374.
Date:                Fri, 25 Apr 2025   Prob (F-statistic):               0.00
Time:                        18:24:32   Log-Likelihood:                -4791.6
No. Observations:                 386   AIC:                             9591.
Df Residuals:                     382   BIC:                             9607.
Df Model:                           3                                         
Covariance Type:            nonrobust                                         
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
const       4.223e+05   8796.875     48.009      0.000    4.05e+05     4.4e+05
x1          4197.2329     80.653     52.041      0.000    4038.653    4355.813
x2          1.776e+04    303.613     58.507      0.000    1.72e+04    1.84e+04
x3         -1.324e+04    295.628    -44.780      0.000   -1.38e+04   -1.27e+04
==============================================================================
Omnibus:                       12.794   Durbin-Watson:                   0.037
Prob(Omnibus):                  0.002   Jarque-Bera (JB):               13.746
Skew:                          -0.383   Prob(JB):                      0.00104
Kurtosis:                       3.517   Cond. No.                         704.
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
3546266303.010624
<Figure size 1200x600 with 1 Axes>

Now we shal fit the same model using PyTorch.

The PiecewiseLinearModel class is a PyTorch neural network module that defines our change of slope model. In the constructor (__init__), it initializes two learnable parameters: beta, a tensor of coefficients (starting with the intercept and slopes), and knots, a tensor representing the locations where slope changes can occur (these are c1,…,ckc_1, \dots, c_k). Both are wrapped as nn.Parameter so they are optimized during training. In the forward method, the knots are first sorted to maintain consistent ordering. The output is then computed by applying an initial linear transformation (beta[0] + beta[1] * x), and adding weighted ReLU activations of the input shifted by each sorted knot (torch.relu(x - knot)), with corresponding weights from beta[2:]. This structure allows the model to learn flexible piecewise linear relationships during optimization.

#Now we shall fit this using a neural network model in pytorch: 
import torch
import torch.nn as nn
import torch.optim as optim

#In this code, we have to supply the initial values for both the knots and the coefficients. 

class PiecewiseLinearModel(nn.Module):
    def __init__(self, knots_init, beta_init):
        super().__init__()
        self.num_knots = len(knots_init)
        self.beta = nn.Parameter(torch.tensor(beta_init, dtype=torch.float32)) 
        self.knots = nn.Parameter(torch.tensor(knots_init, dtype=torch.float32))

    def forward(self, x):
        knots_sorted, _ = torch.sort(self.knots)
        out = self.beta[0] + self.beta[1] * x
        for j in range(self.num_knots):
            out += self.beta[j + 2] * torch.relu(x - knots_sorted[j])
        return out

We do not apply the model to the raw data but we scale the raw data first. The algorithm for parameter fitting will work better with scaled data as opposed to raw data.

The code below first standardizes the raw input arrays y_raw and x_raw by subtracting their means and dividing by their standard deviations, resulting in y_scaled and x_scaled, respectively. This scaling step ensures that both inputs have mean 0 and standard deviation 1, which helps neural network training converge faster and more reliably. After scaling, the arrays are converted into PyTorch tensors (y_torch and x_torch) with dtype=torch.float32, and an additional singleton dimension is added using unsqueeze(1) to ensure each data point is treated as a one-dimensional feature vector. Conversion to PyTorch tensors is necessary because PyTorch models and optimization routines (like gradient computation and parameter updates) operate on tensors, not on NumPy arrays.

#Below we first scale y_raw and x_raw and then convert them to tensors for training the neural network model
y_scaled = (y_raw - np.mean(y_raw))/(np.std(y_raw))
x_scaled = (x_raw - np.mean(x_raw))/(np.std(x_raw))
y_torch = torch.tensor(y_scaled, dtype = torch.float32).unsqueeze(1)
x_torch = torch.tensor(x_scaled, dtype = torch.float32).unsqueeze(1)

Before obtaining parameter estimates via PyTorch, let us first use our older code (from Lecture 9) on the scaled data.

#Older code that we used to fit this model: 
def rss(c):
    n = len(y_scaled)
    x_raw = np.arange(1, n+1)
    x_scaled = (x_raw - np.mean(x_raw))/(np.std(x_raw))
    X = np.column_stack([np.ones(n), x_scaled])
    if np.isscalar(c):
        c = [c]
    for j in range(len(c)):
        xc = ((x_scaled > c[j]).astype(float))*(x_scaled-c[j])
        X = np.column_stack([X, xc])
    md = sm.OLS(y_scaled, X).fit()
    ans = np.sum(md.resid ** 2)
    return ans

c1_gr = np.sort(x_scaled)
c2_gr = np.sort(x_scaled)
X, Y = np.meshgrid(c1_gr, c2_gr)
g = pd.DataFrame({'x': X.flatten(), 'y': Y.flatten()})
g['rss'] = g.apply(lambda row: rss([row['x'], row['y']]), axis = 1)

min_row = g.loc[g['rss'].idxmin()]
print(min_row)
c_opt = min_row[:-1]
print(c_opt)

c = np.array(c_opt)
n = len(y_scaled)
X = np.column_stack([np.ones(n), x_scaled])
if np.isscalar(c):
    c = np.array([c])
for j in range(len(c)):
    xc = ((x_scaled > c[j]).astype(float))*(x_scaled-c[j])
    X = np.column_stack([X, xc])
md_c2 = sm.OLS(y_scaled, X).fit()
print(md_c2.summary())
rss_copt = (np.sum((md_c2.resid ** 2)))/n
print(rss_copt) #this is the smallest value of the loss achieved. 
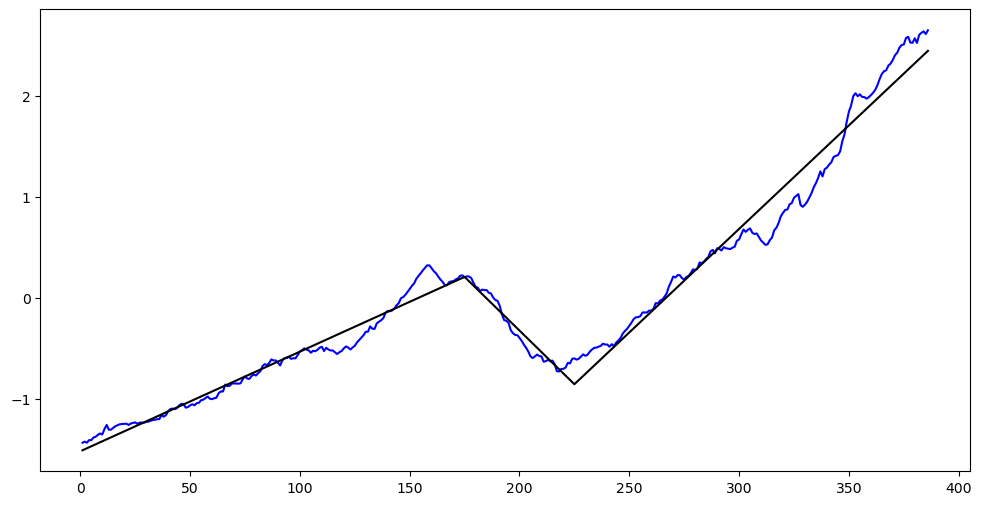
plt.figure(figsize = (12, 6))
plt.plot(tme, y_scaled, color = 'blue')
plt.plot(tme, md_c2.fittedvalues, color = 'black')
plt.show()
x      0.282693
y     -0.166026
rss    7.560319
Name: 67388, dtype: float64
x    0.282693
y   -0.166026
Name: 67388, dtype: float64
                            OLS Regression Results                            
==============================================================================
Dep. Variable:                TTLCONS   R-squared:                       0.980
Model:                            OLS   Adj. R-squared:                  0.980
Method:                 Least Squares   F-statistic:                     6374.
Date:                Fri, 25 Apr 2025   Prob (F-statistic):               0.00
Time:                        18:25:07   Log-Likelihood:                 211.34
No. Observations:                 386   AIC:                            -414.7
Df Residuals:                     382   BIC:                            -398.9
Df Model:                           3                                         
Covariance Type:            nonrobust                                         
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
const          0.3923      0.021     18.414      0.000       0.350       0.434
x1             1.0991      0.021     52.041      0.000       1.058       1.141
x2             4.6518      0.080     58.507      0.000       4.495       4.808
x3            -3.4667      0.077    -44.780      0.000      -3.619      -3.314
==============================================================================
Omnibus:                       12.794   Durbin-Watson:                   0.037
Prob(Omnibus):                  0.002   Jarque-Bera (JB):               13.746
Skew:                          -0.383   Prob(JB):                      0.00104
Kurtosis:                       3.517   Cond. No.                         21.3
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
0.019586318618132627
<Figure size 1200x600 with 1 Axes>

We are now ready to use PyTorch for parameter estimation. The first step is to obtain suitable initial estimates for the parameters. These are deduced as follows. We take c1,…,ckc_1, \dots, c_k to be quantiles of the scaled covariate at equal levels. Then we fit the model with c1,…,ckc_1, \dots, c_k fixed at these initial values, and obtain the initial values of the coefficients.

k = 2 #this is the number of knots
quantile_levels = np.linspace(1/(k+1), k/(k+1), k)
knots_init = np.quantile(x_scaled, quantile_levels)

n = len(y_scaled)
X = np.column_stack([np.ones(n), x_scaled])
for j in range(k):
    xc = ((x_scaled > knots_init[j]).astype(float))*(x_scaled-knots_init[j])  
    X = np.column_stack([X, xc])
md_init = sm.OLS(y_scaled, X).fit()
beta_init = md_init.params.values
print(knots_init)
print(beta_init)

[-0.57585648  0.57585648]
[ 0.56600869  1.2199186  -1.42682417  2.75171746]

The next code line md_nn = PiecewiseLinearModel(knots_init=knots_init, beta_init=beta_init) creates an instance of the custom neural network model PiecewiseLinearModel. It initializes the learnable parameters of the model: the knot locations are set to the values provided in knots_init, and the coefficients are set to beta_init. This prepares the model for training by defining its initial piecewise linear structure.

md_nn = PiecewiseLinearModel(knots_init = knots_init, beta_init = beta_init)
#This code creates an instance of our custom neural network class
#It also initializes the knots at knots_init

The next block of code sets up and runs the training loop for the PiecewiseLinearModel. The Adam optimizer is initialized with the model’s parameters and a learning rate of 0.01, and the loss function is set to mean squared error (MSELoss). For 20,000 epochs, the code repeatedly performs one training step: it clears previous gradients with optimizer.zero_grad(), computes predictions y_pred by passing x_torch through the model, evaluates the loss between predictions and true values, backpropagates the loss with loss.backward(), and updates the model parameters using optimizer.step(). Every 100 epochs, the current epoch and loss value are printed to monitor training progress. Running the code multiple times may be necessary to ensure good convergence, especially for non-convex optimization problems.

optimizer = optim.Adam(md_nn.parameters(), lr = 0.01)
loss_fn = nn.MSELoss()

for epoch in range(20000): 
    optimizer.zero_grad()
    y_pred = md_nn(x_torch)
    loss = loss_fn(y_pred, y_torch)
    loss.backward()
    optimizer.step()
    if epoch % 100 == 0: 
        print(f"Epoch {epoch}, Loss: {loss.item():.4f}")
#Run this code a few times to be sure of convergence. 
Epoch 0, Loss: 0.0429
Epoch 100, Loss: 0.0247
Epoch 200, Loss: 0.0219
Epoch 300, Loss: 0.0207
Epoch 400, Loss: 0.0201
Epoch 500, Loss: 0.0198
Epoch 600, Loss: 0.0197
Epoch 700, Loss: 0.0197
Epoch 800, Loss: 0.0197
Epoch 900, Loss: 0.0196
Epoch 1000, Loss: 0.0196
Epoch 1100, Loss: 0.0196
Epoch 1200, Loss: 0.0196
Epoch 1300, Loss: 0.0196
Epoch 1400, Loss: 0.0196
Epoch 1500, Loss: 0.0196
Epoch 1600, Loss: 0.0196
Epoch 1700, Loss: 0.0196
Epoch 1800, Loss: 0.0196
Epoch 1900, Loss: 0.0196
Epoch 2000, Loss: 0.0196
Epoch 2100, Loss: 0.0196
Epoch 2200, Loss: 0.0196
Epoch 2300, Loss: 0.0196
Epoch 2400, Loss: 0.0196
Epoch 2500, Loss: 0.0196
Epoch 2600, Loss: 0.0196
Epoch 2700, Loss: 0.0196
Epoch 2800, Loss: 0.0196
Epoch 2900, Loss: 0.0196
Epoch 3000, Loss: 0.0196
Epoch 3100, Loss: 0.0196
Epoch 3200, Loss: 0.0196
Epoch 3300, Loss: 0.0196
Epoch 3400, Loss: 0.0196
Epoch 3500, Loss: 0.0196
Epoch 3600, Loss: 0.0196
Epoch 3700, Loss: 0.0196
Epoch 3800, Loss: 0.0196
Epoch 3900, Loss: 0.0196
Epoch 4000, Loss: 0.0196
Epoch 4100, Loss: 0.0196
Epoch 4200, Loss: 0.0196
Epoch 4300, Loss: 0.0196
Epoch 4400, Loss: 0.0196
Epoch 4500, Loss: 0.0196
Epoch 4600, Loss: 0.0196
Epoch 4700, Loss: 0.0196
Epoch 4800, Loss: 0.0196
Epoch 4900, Loss: 0.0196
Epoch 5000, Loss: 0.0196
Epoch 5100, Loss: 0.0196
Epoch 5200, Loss: 0.0196
Epoch 5300, Loss: 0.0196
Epoch 5400, Loss: 0.0196
Epoch 5500, Loss: 0.0196
Epoch 5600, Loss: 0.0196
Epoch 5700, Loss: 0.0196
Epoch 5800, Loss: 0.0196
Epoch 5900, Loss: 0.0196
Epoch 6000, Loss: 0.0196
Epoch 6100, Loss: 0.0196
Epoch 6200, Loss: 0.0196
Epoch 6300, Loss: 0.0196
Epoch 6400, Loss: 0.0196
Epoch 6500, Loss: 0.0196
Epoch 6600, Loss: 0.0196
Epoch 6700, Loss: 0.0196
Epoch 6800, Loss: 0.0196
Epoch 6900, Loss: 0.0196
Epoch 7000, Loss: 0.0196
Epoch 7100, Loss: 0.0196
Epoch 7200, Loss: 0.0197
Epoch 7300, Loss: 0.0196
Epoch 7400, Loss: 0.0196
Epoch 7500, Loss: 0.0196
Epoch 7600, Loss: 0.0196
Epoch 7700, Loss: 0.0197
Epoch 7800, Loss: 0.0196
Epoch 7900, Loss: 0.0196
Epoch 8000, Loss: 0.0196
Epoch 8100, Loss: 0.0196
Epoch 8200, Loss: 0.0196
Epoch 8300, Loss: 0.0196
Epoch 8400, Loss: 0.0196
Epoch 8500, Loss: 0.0196
Epoch 8600, Loss: 0.0196
Epoch 8700, Loss: 0.0196
Epoch 8800, Loss: 0.0196
Epoch 8900, Loss: 0.0196
Epoch 9000, Loss: 0.0196
Epoch 9100, Loss: 0.0196
Epoch 9200, Loss: 0.0197
Epoch 9300, Loss: 0.0196
Epoch 9400, Loss: 0.0196
Epoch 9500, Loss: 0.0196
Epoch 9600, Loss: 0.0196
Epoch 9700, Loss: 0.0196
Epoch 9800, Loss: 0.0196
Epoch 9900, Loss: 0.0196
Epoch 10000, Loss: 0.0196
Epoch 10100, Loss: 0.0196
Epoch 10200, Loss: 0.0196
Epoch 10300, Loss: 0.0196
Epoch 10400, Loss: 0.0196
Epoch 10500, Loss: 0.0196
Epoch 10600, Loss: 0.0196
Epoch 10700, Loss: 0.0196
Epoch 10800, Loss: 0.0196
Epoch 10900, Loss: 0.0196
Epoch 11000, Loss: 0.0196
Epoch 11100, Loss: 0.0196
Epoch 11200, Loss: 0.0196
Epoch 11300, Loss: 0.0196
Epoch 11400, Loss: 0.0196
Epoch 11500, Loss: 0.0196
Epoch 11600, Loss: 0.0196
Epoch 11700, Loss: 0.0196
Epoch 11800, Loss: 0.0196
Epoch 11900, Loss: 0.0196
Epoch 12000, Loss: 0.0196
Epoch 12100, Loss: 0.0196
Epoch 12200, Loss: 0.0196
Epoch 12300, Loss: 0.0196
Epoch 12400, Loss: 0.0196
Epoch 12500, Loss: 0.0196
Epoch 12600, Loss: 0.0196
Epoch 12700, Loss: 0.0196
Epoch 12800, Loss: 0.0196
Epoch 12900, Loss: 0.0196
Epoch 13000, Loss: 0.0196
Epoch 13100, Loss: 0.0196
Epoch 13200, Loss: 0.0196
Epoch 13300, Loss: 0.0196
Epoch 13400, Loss: 0.0196
Epoch 13500, Loss: 0.0196
Epoch 13600, Loss: 0.0196
Epoch 13700, Loss: 0.0196
Epoch 13800, Loss: 0.0196
Epoch 13900, Loss: 0.0196
Epoch 14000, Loss: 0.0196
Epoch 14100, Loss: 0.0196
Epoch 14200, Loss: 0.0196
Epoch 14300, Loss: 0.0196
Epoch 14400, Loss: 0.0196
Epoch 14500, Loss: 0.0196
Epoch 14600, Loss: 0.0196
Epoch 14700, Loss: 0.0196
Epoch 14800, Loss: 0.0196
Epoch 14900, Loss: 0.0196
Epoch 15000, Loss: 0.0196
Epoch 15100, Loss: 0.0196
Epoch 15200, Loss: 0.0196
Epoch 15300, Loss: 0.0196
Epoch 15400, Loss: 0.0196
Epoch 15500, Loss: 0.0196
Epoch 15600, Loss: 0.0196
Epoch 15700, Loss: 0.0196
Epoch 15800, Loss: 0.0196
Epoch 15900, Loss: 0.0196
Epoch 16000, Loss: 0.0196
Epoch 16100, Loss: 0.0196
Epoch 16200, Loss: 0.0196
Epoch 16300, Loss: 0.0196
Epoch 16400, Loss: 0.0196
Epoch 16500, Loss: 0.0196
Epoch 16600, Loss: 0.0196
Epoch 16700, Loss: 0.0196
Epoch 16800, Loss: 0.0196
Epoch 16900, Loss: 0.0196
Epoch 17000, Loss: 0.0196
Epoch 17100, Loss: 0.0196
Epoch 17200, Loss: 0.0196
Epoch 17300, Loss: 0.0196
Epoch 17400, Loss: 0.0196
Epoch 17500, Loss: 0.0196
Epoch 17600, Loss: 0.0196
Epoch 17700, Loss: 0.0196
Epoch 17800, Loss: 0.0196
Epoch 17900, Loss: 0.0196
Epoch 18000, Loss: 0.0196
Epoch 18100, Loss: 0.0196
Epoch 18200, Loss: 0.0196
Epoch 18300, Loss: 0.0196
Epoch 18400, Loss: 0.0196
Epoch 18500, Loss: 0.0196
Epoch 18600, Loss: 0.0196
Epoch 18700, Loss: 0.0196
Epoch 18800, Loss: 0.0196
Epoch 18900, Loss: 0.0197
Epoch 19000, Loss: 0.0196
Epoch 19100, Loss: 0.0196
Epoch 19200, Loss: 0.0196
Epoch 19300, Loss: 0.0196
Epoch 19400, Loss: 0.0196
Epoch 19500, Loss: 0.0196
Epoch 19600, Loss: 0.0196
Epoch 19700, Loss: 0.0196
Epoch 19800, Loss: 0.0196
Epoch 19900, Loss: 0.0196

The next code prints out the current loss value, the estimated model coefficients (beta), and the estimated knot locations after training. The detach().numpy() calls are used to move each tensor from the computation graph to a regular NumPy array so they can be easily printed or further processed without tracking gradients. Finally, it prints rss_copt, which represents the smallest residual sum of squares (RSS) achieved with two knots during training, providing a measure of the model’s fit quality.

print(loss.detach().numpy())
print(md_nn.beta.detach().numpy())
print(md_nn.knots.detach().numpy())
print(rss_copt) #this is the smallest RSS with two knots
0.019580817
[ 0.39307612  1.099781   -3.42655     4.6143637 ]
[-0.16831267  0.2858241 ]
0.019586318618132627

The next code computes the model’s fitted values by passing x_torch through the trained PiecewiseLinearModel and applying .detach().numpy() to convert the output tensor into a NumPy array, which disconnects it from the PyTorch computation graph. The fitted values (nn_fits) represent the model’s predicted outputs on the training data and are printed for inspection.

nn_fits = md_nn(x_torch).detach().numpy()
print(nn_fits)
[[-1.5068719 ]
 [-1.4970021 ]
 [-1.4871321 ]
 [-1.4772625 ]
 [-1.4673924 ]
 [-1.4575226 ]
 [-1.4476528 ]
 [-1.437783  ]
 [-1.4279132 ]
 [-1.4180431 ]
 [-1.4081733 ]
 [-1.3983035 ]
 [-1.3884337 ]
 [-1.3785639 ]
 [-1.3686938 ]
 [-1.358824  ]
 [-1.3489542 ]
 [-1.3390844 ]
 [-1.3292146 ]
 [-1.3193445 ]
 [-1.3094747 ]
 [-1.2996049 ]
 [-1.2897351 ]
 [-1.2798653 ]
 [-1.2699952 ]
 [-1.2601254 ]
 [-1.2502556 ]
 [-1.2403858 ]
 [-1.230516  ]
 [-1.2206461 ]
 [-1.2107761 ]
 [-1.2009063 ]
 [-1.1910365 ]
 [-1.1811666 ]
 [-1.1712968 ]
 [-1.1614268 ]
 [-1.151557  ]
 [-1.1416872 ]
 [-1.1318171 ]
 [-1.1219475 ]
 [-1.1120775 ]
 [-1.1022077 ]
 [-1.0923378 ]
 [-1.082468  ]
 [-1.0725982 ]
 [-1.0627282 ]
 [-1.0528584 ]
 [-1.0429885 ]
 [-1.0331187 ]
 [-1.0232489 ]
 [-1.0133789 ]
 [-1.003509  ]
 [-0.9936393 ]
 [-0.98376936]
 [-0.97389954]
 [-0.9640296 ]
 [-0.9541598 ]
 [-0.94429   ]
 [-0.93442005]
 [-0.92455024]
 [-0.9146803 ]
 [-0.9048105 ]
 [-0.8949407 ]
 [-0.88507074]
 [-0.8752009 ]
 [-0.8653311 ]
 [-0.8554612 ]
 [-0.84559137]
 [-0.83572143]
 [-0.82585174]
 [-0.8159818 ]
 [-0.8061119 ]
 [-0.79624206]
 [-0.7863721 ]
 [-0.7765023 ]
 [-0.7666325 ]
 [-0.75676256]
 [-0.74689275]
 [-0.7370228 ]
 [-0.727153  ]
 [-0.7172832 ]
 [-0.70741326]
 [-0.69754344]
 [-0.6876736 ]
 [-0.6778037 ]
 [-0.6679339 ]
 [-0.65806395]
 [-0.64819413]
 [-0.6383243 ]
 [-0.6284544 ]
 [-0.6185846 ]
 [-0.60871464]
 [-0.5988448 ]
 [-0.588975  ]
 [-0.5791051 ]
 [-0.5692352 ]
 [-0.5593654 ]
 [-0.5494955 ]
 [-0.5396257 ]
 [-0.5297558 ]
 [-0.51988596]
 [-0.5100161 ]
 [-0.50014627]
 [-0.49027634]
 [-0.48040652]
 [-0.47053665]
 [-0.46066678]
 [-0.45079696]
 [-0.44092703]
 [-0.4310572 ]
 [-0.42118734]
 [-0.41131753]
 [-0.4014476 ]
 [-0.39157778]
 [-0.3817079 ]
 [-0.37183803]
 [-0.36196822]
 [-0.3520983 ]
 [-0.34222847]
 [-0.3323586 ]
 [-0.32248878]
 [-0.31261885]
 [-0.30274904]
 [-0.29287916]
 [-0.2830093 ]
 [-0.27313948]
 [-0.26326954]
 [-0.25339973]
 [-0.24352986]
 [-0.23366004]
 [-0.22379011]
 [-0.2139203 ]
 [-0.20405042]
 [-0.19418055]
 [-0.18431073]
 [-0.1744408 ]
 [-0.16457099]
 [-0.15470111]
 [-0.14483124]
 [-0.13496143]
 [-0.12509155]
 [-0.11522168]
 [-0.10535184]
 [-0.09548196]
 [-0.08561212]
 [-0.07574224]
 [-0.0658724 ]
 [-0.0560025 ]
 [-0.04613265]
 [-0.03626278]
 [-0.02639294]
 [-0.01652309]
 [-0.00665322]
 [ 0.00321662]
 [ 0.0130865 ]
 [ 0.02295634]
 [ 0.03282624]
 [ 0.04269609]
 [ 0.05256596]
 [ 0.06243581]
 [ 0.07230568]
 [ 0.08217552]
 [ 0.09204537]
 [ 0.10191524]
 [ 0.11178508]
 [ 0.12165496]
 [ 0.13152483]
 [ 0.14139467]
 [ 0.15126455]
 [ 0.1611344 ]
 [ 0.17100427]
 [ 0.18087412]
 [ 0.190744  ]
 [ 0.20061386]
 [ 0.20264886]
 [ 0.18176754]
 [ 0.1608862 ]
 [ 0.14000489]
 [ 0.11912356]
 [ 0.09824222]
 [ 0.07736091]
 [ 0.05647959]
 [ 0.03559828]
 [ 0.01471692]
 [-0.0061644 ]
 [-0.02704573]
 [-0.04792702]
 [-0.06880838]
 [-0.08968967]
 [-0.110571  ]
 [-0.13145235]
 [-0.15233368]
 [-0.173215  ]
 [-0.1940963 ]
 [-0.21497762]
 [-0.23585892]
 [-0.2567403 ]
 [-0.2776216 ]
 [-0.2985029 ]
 [-0.31938428]
 [-0.3402655 ]
 [-0.3611469 ]
 [-0.3820282 ]
 [-0.40290958]
 [-0.4237908 ]
 [-0.4446721 ]
 [-0.46555346]
 [-0.48643494]
 [-0.5073162 ]
 [-0.5281974 ]
 [-0.54907876]
 [-0.5699601 ]
 [-0.59084153]
 [-0.61172277]
 [-0.632604  ]
 [-0.6534854 ]
 [-0.6743668 ]
 [-0.6952481 ]
 [-0.71612936]
 [-0.7370107 ]
 [-0.75789213]
 [-0.7787733 ]
 [-0.7996546 ]
 [-0.8205361 ]
 [-0.8414173 ]
 [-0.8353348 ]
 [-0.814805  ]
 [-0.79427516]
 [-0.77374554]
 [-0.75321573]
 [-0.7326859 ]
 [-0.7121562 ]
 [-0.6916262 ]
 [-0.67109674]
 [-0.6505669 ]
 [-0.6300372 ]
 [-0.60950744]
 [-0.58897746]
 [-0.56844795]
 [-0.5479181 ]
 [-0.5273882 ]
 [-0.50685865]
 [-0.48632878]
 [-0.46579903]
 [-0.4452694 ]
 [-0.42473948]
 [-0.40420985]
 [-0.38368   ]
 [-0.36315024]
 [-0.3426206 ]
 [-0.32209074]
 [-0.30156088]
 [-0.281031  ]
 [-0.26050138]
 [-0.23997188]
 [-0.21944201]
 [-0.19891214]
 [-0.17838228]
 [-0.15785265]
 [-0.13732302]
 [-0.11679304]
 [-0.09626341]
 [-0.07573342]
 [-0.05520391]
 [-0.03467429]
 [-0.0141443 ]
 [ 0.00638533]
 [ 0.02691531]
 [ 0.04744494]
 [ 0.06797481]
 [ 0.08850443]
 [ 0.10903418]
 [ 0.12956417]
 [ 0.1500938 ]
 [ 0.17062354]
 [ 0.19115329]
 [ 0.21168292]
 [ 0.2322129 ]
 [ 0.25274253]
 [ 0.2732725 ]
 [ 0.29380202]
 [ 0.31433177]
 [ 0.33486128]
 [ 0.35539126]
 [ 0.37592125]
 [ 0.39645076]
 [ 0.4169805 ]
 [ 0.43751073]
 [ 0.45804024]
 [ 0.47857022]
 [ 0.49909925]
 [ 0.51962924]
 [ 0.54015946]
 [ 0.56068873]
 [ 0.58121896]
 [ 0.60174847]
 [ 0.622278  ]
 [ 0.6428082 ]
 [ 0.6633377 ]
 [ 0.6838677 ]
 [ 0.7043967 ]
 [ 0.7249272 ]
 [ 0.74545693]
 [ 0.76598644]
 [ 0.7865162 ]
 [ 0.8070462 ]
 [ 0.8275759 ]
 [ 0.8481059 ]
 [ 0.8686354 ]
 [ 0.88916516]
 [ 0.90969515]
 [ 0.9302244 ]
 [ 0.9507544 ]
 [ 0.9712844 ]
 [ 0.9918139 ]
 [ 1.0123436 ]
 [ 1.0328739 ]
 [ 1.0534034 ]
 [ 1.0739331 ]
 [ 1.0944629 ]
 [ 1.1149929 ]
 [ 1.1355224 ]
 [ 1.1560519 ]
 [ 1.1765821 ]
 [ 1.1971116 ]
 [ 1.2176411 ]
 [ 1.2381711 ]
 [ 1.2587011 ]
 [ 1.2792308 ]
 [ 1.2997603 ]
 [ 1.3202903 ]
 [ 1.3408203 ]
 [ 1.3613493 ]
 [ 1.3818796 ]
 [ 1.4024096 ]
 [ 1.4229391 ]
 [ 1.4434686 ]
 [ 1.4639986 ]
 [ 1.4845283 ]
 [ 1.5050583 ]
 [ 1.5255878 ]
 [ 1.5461178 ]
 [ 1.5666473 ]
 [ 1.5871768 ]
 [ 1.607707  ]
 [ 1.6282365 ]
 [ 1.6487665 ]
 [ 1.669296  ]
 [ 1.6898255 ]
 [ 1.7103558 ]
 [ 1.7308853 ]
 [ 1.7514153 ]
 [ 1.7719448 ]
 [ 1.7924747 ]
 [ 1.8130045 ]
 [ 1.833534  ]
 [ 1.854064  ]
 [ 1.874594  ]
 [ 1.895123  ]
 [ 1.9156532 ]
 [ 1.9361832 ]
 [ 1.9567127 ]
 [ 1.9772422 ]
 [ 1.9977722 ]
 [ 2.0183024 ]
 [ 2.0388312 ]
 [ 2.0593615 ]
 [ 2.0798914 ]
 [ 2.1004214 ]
 [ 2.1209507 ]
 [ 2.1414807 ]
 [ 2.1620107 ]
 [ 2.1825402 ]
 [ 2.2030697 ]
 [ 2.2236    ]
 [ 2.24413   ]
 [ 2.264659  ]
 [ 2.2851892 ]
 [ 2.305719  ]
 [ 2.3262482 ]
 [ 2.3467784 ]
 [ 2.3673081 ]
 [ 2.3878374 ]
 [ 2.4083672 ]
 [ 2.428897  ]
 [ 2.4494276 ]]

plt.figure(figsize = (12, 6))
plt.plot(x_scaled, y_scaled, color = 'blue', label = 'Data')
plt.plot(x_scaled, md_c2.fittedvalues, color = 'black', label = 'Fitted Values')
plt.plot(x_scaled, nn_fits, color = 'red', label = 'PyTorch Fitted Values')
plt.legend()
plt.show()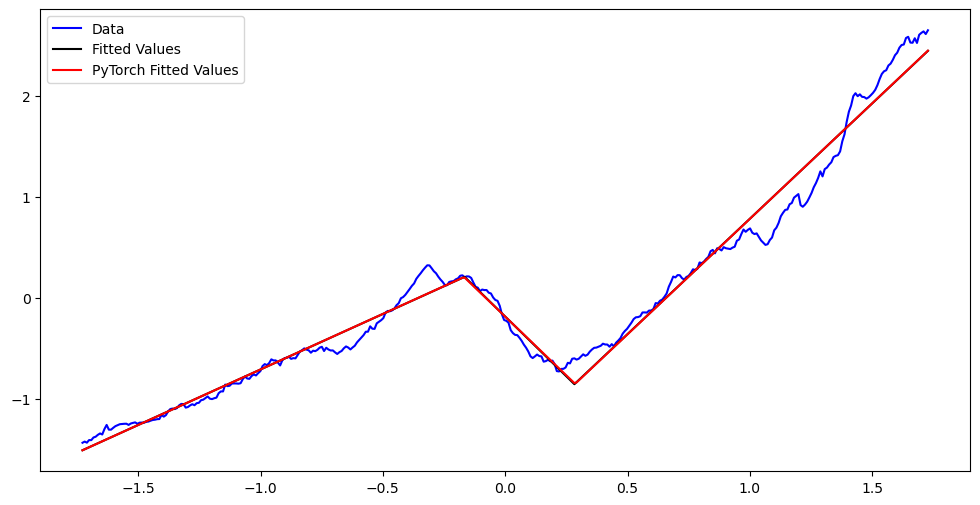
<Figure size 1200x600 with 1 Axes>

Larger number of knots and Regularization

Below we apply the code for kk larger than 2. First we take k=6k = 6.

k = 6 #this is the number of knots
quantile_levels = np.linspace(1/(k+1), k/(k+1), k)
knots_init = np.quantile(x_scaled, quantile_levels)

n = len(y_scaled)
X = np.column_stack([np.ones(n), x_scaled])
for j in range(k):
    xc = ((x_scaled > knots_init[j]).astype(float))*(x_scaled-knots_init[j])  
    X = np.column_stack([X, xc])
md_init = sm.OLS(y_scaled, X).fit()
beta_init = md_init.params.values
print(knots_init)
print(beta_init)
[-1.23397816 -0.7403869  -0.24679563  0.24679563  0.7403869   1.23397816]
[ 0.15436343  0.91474382 -0.0392841   0.85800737 -3.89942     4.1298293
 -0.33642219  2.10097127]

md_nn = PiecewiseLinearModel(knots_init = knots_init, beta_init = beta_init)
#This code creates an instance of our custom neural network class
#It also initializes the knots at knots_init
optimizer = optim.Adam(md_nn.parameters(), lr = 0.01)
loss_fn = nn.MSELoss()

for epoch in range(20000): 
    optimizer.zero_grad()
    y_pred = md_nn(x_torch)
    loss = loss_fn(y_pred, y_torch)
    loss.backward()
    optimizer.step()
    if epoch % 100 == 0: 
        print(f"Epoch {epoch}, Loss: {loss.item():.4f}")
#Run this code a few times to be sure of convergence. 
Epoch 0, Loss: 0.0057
Epoch 100, Loss: 0.0051
Epoch 200, Loss: 0.0049
Epoch 300, Loss: 0.0049
Epoch 400, Loss: 0.0048
Epoch 500, Loss: 0.0047
Epoch 600, Loss: 0.0047
Epoch 700, Loss: 0.0046
Epoch 800, Loss: 0.0046
Epoch 900, Loss: 0.0045
Epoch 1000, Loss: 0.0045
Epoch 1100, Loss: 0.0045
Epoch 1200, Loss: 0.0044
Epoch 1300, Loss: 0.0044
Epoch 1400, Loss: 0.0044
Epoch 1500, Loss: 0.0045
Epoch 1600, Loss: 0.0044
Epoch 1700, Loss: 0.0044
Epoch 1800, Loss: 0.0044
Epoch 1900, Loss: 0.0043
Epoch 2000, Loss: 0.0044
Epoch 2100, Loss: 0.0043
Epoch 2200, Loss: 0.0043
Epoch 2300, Loss: 0.0043
Epoch 2400, Loss: 0.0043
Epoch 2500, Loss: 0.0043
Epoch 2600, Loss: 0.0043
Epoch 2700, Loss: 0.0042
Epoch 2800, Loss: 0.0043
Epoch 2900, Loss: 0.0042
Epoch 3000, Loss: 0.0042
Epoch 3100, Loss: 0.0042
Epoch 3200, Loss: 0.0042
Epoch 3300, Loss: 0.0042
Epoch 3400, Loss: 0.0042
Epoch 3500, Loss: 0.0042
Epoch 3600, Loss: 0.0042
Epoch 3700, Loss: 0.0042
Epoch 3800, Loss: 0.0044
Epoch 3900, Loss: 0.0042
Epoch 4000, Loss: 0.0042
Epoch 4100, Loss: 0.0041
Epoch 4200, Loss: 0.0041
Epoch 4300, Loss: 0.0042
Epoch 4400, Loss: 0.0041
Epoch 4500, Loss: 0.0041
Epoch 4600, Loss: 0.0042
Epoch 4700, Loss: 0.0041
Epoch 4800, Loss: 0.0041
Epoch 4900, Loss: 0.0041
Epoch 5000, Loss: 0.0041
Epoch 5100, Loss: 0.0041
Epoch 5200, Loss: 0.0041
Epoch 5300, Loss: 0.0041
Epoch 5400, Loss: 0.0041
Epoch 5500, Loss: 0.0041
Epoch 5600, Loss: 0.0041
Epoch 5700, Loss: 0.0043
Epoch 5800, Loss: 0.0041
Epoch 5900, Loss: 0.0041
Epoch 6000, Loss: 0.0041
Epoch 6100, Loss: 0.0041
Epoch 6200, Loss: 0.0041
Epoch 6300, Loss: 0.0041
Epoch 6400, Loss: 0.0041
Epoch 6500, Loss: 0.0041
Epoch 6600, Loss: 0.0041
Epoch 6700, Loss: 0.0041
Epoch 6800, Loss: 0.0041
Epoch 6900, Loss: 0.0041
Epoch 7000, Loss: 0.0041
Epoch 7100, Loss: 0.0041
Epoch 7200, Loss: 0.0041
Epoch 7300, Loss: 0.0045
Epoch 7400, Loss: 0.0041
Epoch 7500, Loss: 0.0041
Epoch 7600, Loss: 0.0041
Epoch 7700, Loss: 0.0041
Epoch 7800, Loss: 0.0041
Epoch 7900, Loss: 0.0040
Epoch 8000, Loss: 0.0040
Epoch 8100, Loss: 0.0040
Epoch 8200, Loss: 0.0040
Epoch 8300, Loss: 0.0040
Epoch 8400, Loss: 0.0041
Epoch 8500, Loss: 0.0041
Epoch 8600, Loss: 0.0040
Epoch 8700, Loss: 0.0040
Epoch 8800, Loss: 0.0040
Epoch 8900, Loss: 0.0040
Epoch 9000, Loss: 0.0040
Epoch 9100, Loss: 0.0040
Epoch 9200, Loss: 0.0041
Epoch 9300, Loss: 0.0040
Epoch 9400, Loss: 0.0040
Epoch 9500, Loss: 0.0040
Epoch 9600, Loss: 0.0040
Epoch 9700, Loss: 0.0040
Epoch 9800, Loss: 0.0040
Epoch 9900, Loss: 0.0040
Epoch 10000, Loss: 0.0040
Epoch 10100, Loss: 0.0040
Epoch 10200, Loss: 0.0040
Epoch 10300, Loss: 0.0040
Epoch 10400, Loss: 0.0040
Epoch 10500, Loss: 0.0040
Epoch 10600, Loss: 0.0040
Epoch 10700, Loss: 0.0040
Epoch 10800, Loss: 0.0040
Epoch 10900, Loss: 0.0040
Epoch 11000, Loss: 0.0040
Epoch 11100, Loss: 0.0040
Epoch 11200, Loss: 0.0041
Epoch 11300, Loss: 0.0040
Epoch 11400, Loss: 0.0040
Epoch 11500, Loss: 0.0041
Epoch 11600, Loss: 0.0040
Epoch 11700, Loss: 0.0040
Epoch 11800, Loss: 0.0040
Epoch 11900, Loss: 0.0040
Epoch 12000, Loss: 0.0040
Epoch 12100, Loss: 0.0040
Epoch 12200, Loss: 0.0040
Epoch 12300, Loss: 0.0040
Epoch 12400, Loss: 0.0040
Epoch 12500, Loss: 0.0040
Epoch 12600, Loss: 0.0040
Epoch 12700, Loss: 0.0040
Epoch 12800, Loss: 0.0040
Epoch 12900, Loss: 0.0040
Epoch 13000, Loss: 0.0041
Epoch 13100, Loss: 0.0040
Epoch 13200, Loss: 0.0040
Epoch 13300, Loss: 0.0040
Epoch 13400, Loss: 0.0040
Epoch 13500, Loss: 0.0040
Epoch 13600, Loss: 0.0040
Epoch 13700, Loss: 0.0040
Epoch 13800, Loss: 0.0041
Epoch 13900, Loss: 0.0040
Epoch 14000, Loss: 0.0040
Epoch 14100, Loss: 0.0040
Epoch 14200, Loss: 0.0040
Epoch 14300, Loss: 0.0040
Epoch 14400, Loss: 0.0040
Epoch 14500, Loss: 0.0041
Epoch 14600, Loss: 0.0042
Epoch 14700, Loss: 0.0040
Epoch 14800, Loss: 0.0040
Epoch 14900, Loss: 0.0040
Epoch 15000, Loss: 0.0040
Epoch 15100, Loss: 0.0040
Epoch 15200, Loss: 0.0040
Epoch 15300, Loss: 0.0040
Epoch 15400, Loss: 0.0040
Epoch 15500, Loss: 0.0040
Epoch 15600, Loss: 0.0040
Epoch 15700, Loss: 0.0040
Epoch 15800, Loss: 0.0040
Epoch 15900, Loss: 0.0040
Epoch 16000, Loss: 0.0041
Epoch 16100, Loss: 0.0040
Epoch 16200, Loss: 0.0040
Epoch 16300, Loss: 0.0040
Epoch 16400, Loss: 0.0040
Epoch 16500, Loss: 0.0040
Epoch 16600, Loss: 0.0042
Epoch 16700, Loss: 0.0040
Epoch 16800, Loss: 0.0040
Epoch 16900, Loss: 0.0040
Epoch 17000, Loss: 0.0040
Epoch 17100, Loss: 0.0040
Epoch 17200, Loss: 0.0040
Epoch 17300, Loss: 0.0040
Epoch 17400, Loss: 0.0040
Epoch 17500, Loss: 0.0040
Epoch 17600, Loss: 0.0040
Epoch 17700, Loss: 0.0040
Epoch 17800, Loss: 0.0040
Epoch 17900, Loss: 0.0047
Epoch 18000, Loss: 0.0040
Epoch 18100, Loss: 0.0040
Epoch 18200, Loss: 0.0041
Epoch 18300, Loss: 0.0040
Epoch 18400, Loss: 0.0040
Epoch 18500, Loss: 0.0041
Epoch 18600, Loss: 0.0040
Epoch 18700, Loss: 0.0040
Epoch 18800, Loss: 0.0040
Epoch 18900, Loss: 0.0040
Epoch 19000, Loss: 0.0040
Epoch 19100, Loss: 0.0040
Epoch 19200, Loss: 0.0040
Epoch 19300, Loss: 0.0040
Epoch 19400, Loss: 0.0040
Epoch 19500, Loss: 0.0040
Epoch 19600, Loss: 0.0045
Epoch 19700, Loss: 0.0040
Epoch 19800, Loss: 0.0040
Epoch 19900, Loss: 0.0040

print(loss.detach().numpy())
print(md_nn.beta.detach().numpy())
print(md_nn.knots.detach().numpy())
print(rss_copt) #this is the smallest RSS with two knots
0.004008136
[ 0.2617606   0.9924645  -0.81128037  2.1586957  -4.6034064   4.16186
 -3.8148813   5.3695893 ]
[-0.7957666  -0.6338984  -0.26267192  0.2348822   0.99296016  1.0693403 ]
0.019586318618132627

nn_fits = md_nn(x_torch).detach().numpy()
print(nn_fits)
[[-1.45279074e+00]
 [-1.44388390e+00]
 [-1.43497717e+00]
 [-1.42607045e+00]
 [-1.41716361e+00]
 [-1.40825689e+00]
 [-1.39935017e+00]
 [-1.39044333e+00]
 [-1.38153660e+00]
 [-1.37262988e+00]
 [-1.36372316e+00]
 [-1.35481632e+00]
 [-1.34590960e+00]
 [-1.33700287e+00]
 [-1.32809603e+00]
 [-1.31918931e+00]
 [-1.31028259e+00]
 [-1.30137575e+00]
 [-1.29246902e+00]
 [-1.28356230e+00]
 [-1.27465546e+00]
 [-1.26574874e+00]
 [-1.25684190e+00]
 [-1.24793530e+00]
 [-1.23902845e+00]
 [-1.23012161e+00]
 [-1.22121501e+00]
 [-1.21230817e+00]
 [-1.20340145e+00]
 [-1.19449472e+00]
 [-1.18558788e+00]
 [-1.17668116e+00]
 [-1.16777432e+00]
 [-1.15886772e+00]
 [-1.14996088e+00]
 [-1.14105403e+00]
 [-1.13214743e+00]
 [-1.12324059e+00]
 [-1.11433375e+00]
 [-1.10542703e+00]
 [-1.09652030e+00]
 [-1.08761358e+00]
 [-1.07870674e+00]
 [-1.06980002e+00]
 [-1.06089330e+00]
 [-1.05198646e+00]
 [-1.04307985e+00]
 [-1.03417301e+00]
 [-1.02526617e+00]
 [-1.01635945e+00]
 [-1.00745273e+00]
 [-9.98546004e-01]
 [-9.89639163e-01]
 [-9.80732441e-01]
 [-9.71825719e-01]
 [-9.62918878e-01]
 [-9.54012036e-01]
 [-9.45105433e-01]
 [-9.36198592e-01]
 [-9.27291870e-01]
 [-9.18385148e-01]
 [-9.09478307e-01]
 [-9.00571585e-01]
 [-8.91664863e-01]
 [-8.82758141e-01]
 [-8.73851299e-01]
 [-8.64944458e-01]
 [-8.56037855e-01]
 [-8.47131014e-01]
 [-8.38224292e-01]
 [-8.29317570e-01]
 [-8.20410728e-01]
 [-8.11504006e-01]
 [-8.02597165e-01]
 [-7.93690443e-01]
 [-7.84783721e-01]
 [-7.75876880e-01]
 [-7.66970277e-01]
 [-7.58063436e-01]
 [-7.49156594e-01]
 [-7.40249872e-01]
 [-7.31343150e-01]
 [-7.22436368e-01]
 [-7.13529646e-01]
 [-7.04622865e-01]
 [-6.95716083e-01]
 [-6.86809361e-01]
 [-6.77902579e-01]
 [-6.68995857e-01]
 [-6.60089076e-01]
 [-6.51182294e-01]
 [-6.42275512e-01]
 [-6.33368790e-01]
 [-6.24462068e-01]
 [-6.15555227e-01]
 [-6.06648505e-01]
 [-5.97741723e-01]
 [-5.88835001e-01]
 [-5.79928279e-01]
 [-5.71021438e-01]
 [-5.62114716e-01]
 [-5.53207934e-01]
 [-5.44301212e-01]
 [-5.35394371e-01]
 [-5.27731657e-01]
 [-5.26105642e-01]
 [-5.24479628e-01]
 [-5.22853613e-01]
 [-5.21227598e-01]
 [-5.19601583e-01]
 [-5.17975569e-01]
 [-5.16349554e-01]
 [-5.14723539e-01]
 [-5.13097525e-01]
 [-5.11471510e-01]
 [-5.09845495e-01]
 [-5.08219481e-01]
 [-5.06593466e-01]
 [-5.04967391e-01]
 [-5.03341436e-01]
 [-5.01715362e-01]
 [-5.00089407e-01]
 [-4.95864034e-01]
 [-4.74865049e-01]
 [-4.53866124e-01]
 [-4.32867110e-01]
 [-4.11868036e-01]
 [-3.90869141e-01]
 [-3.69870126e-01]
 [-3.48871231e-01]
 [-3.27872068e-01]
 [-3.06873143e-01]
 [-2.85874158e-01]
 [-2.64875203e-01]
 [-2.43876308e-01]
 [-2.22877175e-01]
 [-2.01878250e-01]
 [-1.80879265e-01]
 [-1.59880221e-01]
 [-1.38881266e-01]
 [-1.17882252e-01]
 [-9.68833268e-02]
 [-7.58843720e-02]
 [-5.48853278e-02]
 [-3.38863730e-02]
 [-1.28873587e-02]
 [ 8.11159611e-03]
 [ 2.91106403e-02]
 [ 5.01095653e-02]
 [ 7.11085796e-02]
 [ 9.21075344e-02]
 [ 1.13106489e-01]
 [ 1.34105593e-01]
 [ 1.55104518e-01]
 [ 1.76103532e-01]
 [ 1.97102487e-01]
 [ 2.18101531e-01]
 [ 2.39100486e-01]
 [ 2.60099471e-01]
 [ 2.81098425e-01]
 [ 3.02097470e-01]
 [ 3.23096395e-01]
 [ 3.44095409e-01]
 [ 3.65094393e-01]
 [ 3.54321122e-01]
 [ 3.34007382e-01]
 [ 3.13693583e-01]
 [ 2.93379843e-01]
 [ 2.73066044e-01]
 [ 2.52752304e-01]
 [ 2.32438534e-01]
 [ 2.12124795e-01]
 [ 1.91810995e-01]
 [ 1.71497256e-01]
 [ 1.51183456e-01]
 [ 1.30869776e-01]
 [ 1.10556006e-01]
 [ 9.02421474e-02]
 [ 6.99283481e-02]
 [ 4.96147871e-02]
 [ 2.93009877e-02]
 [ 8.98718834e-03]
 [-1.13265514e-02]
 [-3.16404104e-02]
 [-5.19540310e-02]
 [-7.22678900e-02]
 [-9.25816298e-02]
 [-1.12895429e-01]
 [-1.33209229e-01]
 [-1.53522849e-01]
 [-1.73836708e-01]
 [-1.94150448e-01]
 [-2.14464307e-01]
 [-2.34777927e-01]
 [-2.55091786e-01]
 [-2.75405526e-01]
 [-2.95719385e-01]
 [-3.16033006e-01]
 [-3.36346745e-01]
 [-3.56660604e-01]
 [-3.76974225e-01]
 [-3.97288203e-01]
 [-4.17601824e-01]
 [-4.37915683e-01]
 [-4.58229423e-01]
 [-4.78543282e-01]
 [-4.98857021e-01]
 [-5.19170642e-01]
 [-5.39484382e-01]
 [-5.59798360e-01]
 [-5.80111980e-01]
 [-6.00425720e-01]
 [-6.20739460e-01]
 [-6.41053438e-01]
 [-6.61367178e-01]
 [-6.81680799e-01]
 [-7.01994419e-01]
 [-7.22308517e-01]
 [-7.42622137e-01]
 [-7.50703990e-01]
 [-7.33667433e-01]
 [-7.16630936e-01]
 [-6.99594796e-01]
 [-6.82558358e-01]
 [-6.65521979e-01]
 [-6.48485661e-01]
 [-6.31449342e-01]
 [-6.14413083e-01]
 [-5.97376347e-01]
 [-5.80340266e-01]
 [-5.63303828e-01]
 [-5.46267211e-01]
 [-5.29230952e-01]
 [-5.12194753e-01]
 [-4.95157957e-01]
 [-4.78122056e-01]
 [-4.61085618e-01]
 [-4.44049239e-01]
 [-4.27012682e-01]
 [-4.09976304e-01]
 [-3.92940104e-01]
 [-3.75903368e-01]
 [-3.58867288e-01]
 [-3.41830790e-01]
 [-3.24794233e-01]
 [-3.07758093e-01]
 [-2.90721655e-01]
 [-2.73685336e-01]
 [-2.56649017e-01]
 [-2.39612460e-01]
 [-2.22576380e-01]
 [-2.05539823e-01]
 [-1.88503385e-01]
 [-1.71467066e-01]
 [-1.54430509e-01]
 [-1.37394428e-01]
 [-1.20357990e-01]
 [-1.03321195e-01]
 [-8.62853527e-02]
 [-6.92487955e-02]
 [-5.22121191e-02]
 [-3.51762772e-02]
 [-1.81397200e-02]
 [-1.10363960e-03]
 [ 1.59331560e-02]
 [ 3.29693556e-02]
 [ 5.00056744e-02]
 [ 6.70422316e-02]
 [ 8.40783119e-02]
 [ 1.01114750e-01]
 [ 1.18151546e-01]
 [ 1.35187387e-01]
 [ 1.52223945e-01]
 [ 1.69260025e-01]
 [ 1.86296940e-01]
 [ 2.03333139e-01]
 [ 2.20369577e-01]
 [ 2.37406015e-01]
 [ 2.54442692e-01]
 [ 2.71478415e-01]
 [ 2.88515806e-01]
 [ 3.05551052e-01]
 [ 3.22587967e-01]
 [ 3.39624643e-01]
 [ 3.56660604e-01]
 [ 3.73696804e-01]
 [ 3.90733242e-01]
 [ 4.07769680e-01]
 [ 4.24806356e-01]
 [ 4.41842079e-01]
 [ 4.58879232e-01]
 [ 4.75914955e-01]
 [ 4.92951632e-01]
 [ 5.09988070e-01]
 [ 5.27024269e-01]
 [ 5.44060707e-01]
 [ 5.61097622e-01]
 [ 5.78133106e-01]
 [ 5.95170021e-01]
 [ 6.12205744e-01]
 [ 6.29243374e-01]
 [ 6.46278858e-01]
 [ 6.63315296e-01]
 [ 6.80351973e-01]
 [ 6.68074906e-01]
 [ 6.50874436e-01]
 [ 6.33674920e-01]
 [ 6.16474986e-01]
 [ 5.99275231e-01]
 [ 5.82075059e-01]
 [ 5.64875543e-01]
 [ 5.47675610e-01]
 [ 5.47115386e-01]
 [ 5.78104615e-01]
 [ 6.09093070e-01]
 [ 6.40082359e-01]
 [ 6.71071649e-01]
 [ 7.02060103e-01]
 [ 7.33049393e-01]
 [ 7.64037549e-01]
 [ 7.95027137e-01]
 [ 8.26015890e-01]
 [ 8.57004762e-01]
 [ 8.87993574e-01]
 [ 9.18982446e-01]
 [ 9.49971318e-01]
 [ 9.80960548e-01]
 [ 1.01194930e+00]
 [ 1.04293847e+00]
 [ 1.07392693e+00]
 [ 1.10491621e+00]
 [ 1.13590455e+00]
 [ 1.16689396e+00]
 [ 1.19788277e+00]
 [ 1.22887158e+00]
 [ 1.25986040e+00]
 [ 1.29084992e+00]
 [ 1.32183790e+00]
 [ 1.35282791e+00]
 [ 1.38381648e+00]
 [ 1.41480541e+00]
 [ 1.44579434e+00]
 [ 1.47678339e+00]
 [ 1.50777197e+00]
 [ 1.53876042e+00]
 [ 1.56975031e+00]
 [ 1.60073888e+00]
 [ 1.63172734e+00]
 [ 1.66271734e+00]
 [ 1.69370592e+00]
 [ 1.72469425e+00]
 [ 1.75568390e+00]
 [ 1.78667247e+00]
 [ 1.81766176e+00]
 [ 1.84865034e+00]
 [ 1.87963879e+00]
 [ 1.91062832e+00]
 [ 1.94161725e+00]
 [ 1.97260523e+00]
 [ 2.00359488e+00]
 [ 2.03458309e+00]
 [ 2.06557226e+00]
 [ 2.09656215e+00]
 [ 2.12755084e+00]
 [ 2.15853977e+00]
 [ 2.18952918e+00]
 [ 2.22051716e+00]
 [ 2.25150633e+00]
 [ 2.28249550e+00]
 [ 2.31348419e+00]
 [ 2.34447265e+00]
 [ 2.37546206e+00]
 [ 2.40645075e+00]
 [ 2.43744016e+00]
 [ 2.46842861e+00]
 [ 2.49941730e+00]
 [ 2.53040671e+00]
 [ 2.56139565e+00]
 [ 2.59238362e+00]
 [ 2.62337255e+00]
 [ 2.65436292e+00]
 [ 2.68535066e+00]
 [ 2.71634030e+00]
 [ 2.74732852e+00]
 [ 2.77831817e+00]
 [ 2.80930758e+00]]

plt.figure(figsize = (12, 6))
plt.plot(x_scaled, y_scaled, color = 'blue', label = 'Data')
#plt.plot(x_scaled, md_c2.fittedvalues, color = 'black', label = 'Fitted Values')
plt.plot(x_scaled, nn_fits, color = 'red', label = 'PyTorch Fitted Values')
plt.legend()
plt.show()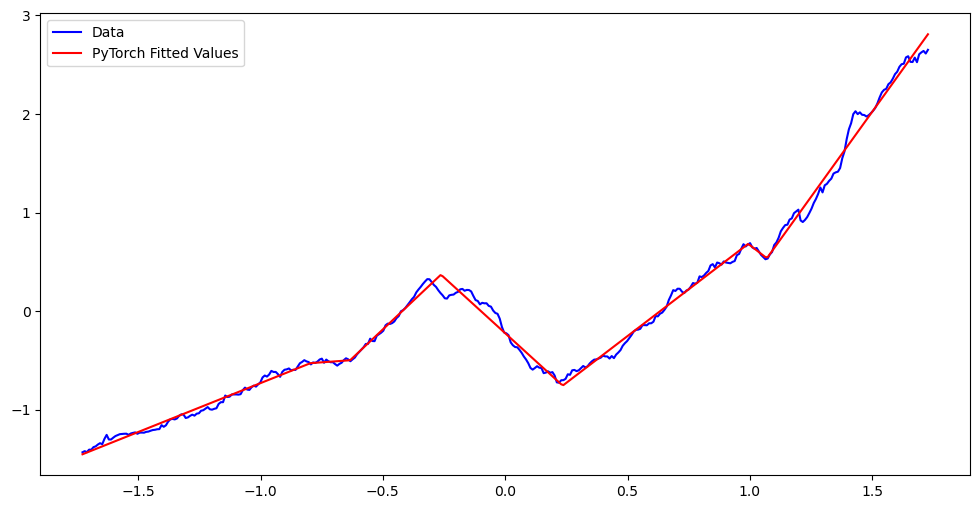
<Figure size 1200x600 with 1 Axes>

Remember that previously we were not quite able to fit the model for k=6k = 6. The number of unknown knots c1,…,ckc_1, \dots, c_k was too big to do a brute force search. Next we take kk to be a larger number (k=50k = 50) and apply the method. Here we need to add regularization otherwise the model will essentially overfit the data. We will use the same regularization that we previously used (L1L_1 norm of the coefficients).

k = 50 #this is the number of knots
quantile_levels = np.linspace(1/(k+1), k/(k+1), k)
knots_init = np.quantile(x_scaled, quantile_levels)

n = len(y_scaled)
X = np.column_stack([np.ones(n), x_scaled])
for j in range(k):
    xc = ((x_scaled > knots_init[j]).astype(float))*(x_scaled-knots_init[j])  
    X = np.column_stack([X, xc])
md_init = sm.OLS(y_scaled, X).fit()
beta_init = md_init.params.values
print(knots_init)
print(beta_init)
[-1.65982161 -1.59207379 -1.52432596 -1.45657814 -1.38883032 -1.3210825
 -1.25333468 -1.18558686 -1.11783904 -1.05009122 -0.9823434  -0.91459558
 -0.84684776 -0.77909994 -0.71135212 -0.6436043  -0.57585648 -0.50810865
 -0.44036083 -0.37261301 -0.30486519 -0.23711737 -0.16936955 -0.10162173
 -0.03387391  0.03387391  0.10162173  0.16936955  0.23711737  0.30486519
  0.37261301  0.44036083  0.50810865  0.57585648  0.6436043   0.71135212
  0.77909994  0.84684776  0.91459558  0.9823434   1.05009122  1.11783904
  1.18558686  1.25333468  1.3210825   1.38883032  1.45657814  1.52432596
  1.59207379  1.65982161]
[ 1.03030663e+00  1.43189061e+00 -1.58045417e-01 -9.62720527e-01
 -1.59327404e-01  1.03424172e+00  9.27391404e-02 -8.99195890e-01
  5.36868641e-01  9.76505452e-01 -1.29730204e+00  1.55448090e+00
 -1.60634200e+00  5.00523979e-01 -3.03969836e-01 -1.02428612e+00
  3.60217386e-01  2.15826811e+00 -2.02834481e-03 -4.97160969e-02
  1.18893426e+00 -9.17836279e-01 -5.60822348e+00  5.00254824e+00
 -3.97505659e+00  2.83700037e-01 -2.89079116e+00  1.77801190e+00
  1.95314550e+00 -2.97522039e-01  3.13128617e+00 -3.47668918e-01
 -1.39616376e+00  3.10323751e+00 -1.46600236e+00  4.24166888e-01
  1.18778916e+00 -2.80811642e+00  2.60696113e+00 -3.25517403e+00
  3.49848985e+00 -5.89071541e+00  5.67508201e+00  3.21580853e-01
 -2.73275273e+00  3.17023476e+00  1.78417258e+00 -3.72125063e-01
 -4.71313810e+00  4.46631782e+00 -3.14388593e+00 -7.78212643e-01]

md_nn = PiecewiseLinearModel(knots_init = knots_init, beta_init = beta_init)
#Adding a regularizer to the loss function.
optimizer = optim.Adam(md_nn.parameters(), lr = 0.01)
loss_fn = nn.MSELoss()
lambda_l1 = 0.001 #this works pretty well
#lambda_l2 = .002

for epoch in range(30000): 
    optimizer.zero_grad()
    y_pred = md_nn(x_torch)
    mse_loss = loss_fn(y_pred, y_torch)
    l1_penalty = torch.norm(md_nn.beta[2:], p = 1) 
    #l2_penalty = torch.sum(md_nn.beta[2:] ** 2)
    loss = mse_loss + lambda_l1 * l1_penalty
    #loss = mse_loss + lambda_l2 * l2_penalty
    loss.backward()
    optimizer.step()
    if epoch % 100 == 0: 
        print(f"Epoch {epoch}, Loss: {loss.item():.4f}")
#Run this code a few times to be sure of convergence. 
Epoch 0, Loss: 0.0947
Epoch 100, Loss: 0.0921
Epoch 200, Loss: 0.0902
Epoch 300, Loss: 0.0880
Epoch 400, Loss: 0.0856
Epoch 500, Loss: 0.0830
Epoch 600, Loss: 0.0807
Epoch 700, Loss: 0.0784
Epoch 800, Loss: 0.0759
Epoch 900, Loss: 0.0734
Epoch 1000, Loss: 0.0712
Epoch 1100, Loss: 0.0692
Epoch 1200, Loss: 0.0673
Epoch 1300, Loss: 0.0654
Epoch 1400, Loss: 0.0634
Epoch 1500, Loss: 0.0614
Epoch 1600, Loss: 0.0594
Epoch 1700, Loss: 0.0575
Epoch 1800, Loss: 0.0557
Epoch 1900, Loss: 0.0539
Epoch 2000, Loss: 0.0521
Epoch 2100, Loss: 0.0511
Epoch 2200, Loss: 0.0489
Epoch 2300, Loss: 0.0475
Epoch 2400, Loss: 0.0460
Epoch 2500, Loss: 0.0445
Epoch 2600, Loss: 0.0430
Epoch 2700, Loss: 0.0414
Epoch 2800, Loss: 0.0398
Epoch 2900, Loss: 0.0382
Epoch 3000, Loss: 0.0368
Epoch 3100, Loss: 0.0354
Epoch 3200, Loss: 0.0342
Epoch 3300, Loss: 0.0331
Epoch 3400, Loss: 0.0322
Epoch 3500, Loss: 0.0316
Epoch 3600, Loss: 0.0310
Epoch 3700, Loss: 0.0306
Epoch 3800, Loss: 0.0301
Epoch 3900, Loss: 0.0297
Epoch 4000, Loss: 0.0292
Epoch 4100, Loss: 0.0288
Epoch 4200, Loss: 0.0285
Epoch 4300, Loss: 0.0287
Epoch 4400, Loss: 0.0278
Epoch 4500, Loss: 0.0275
Epoch 4600, Loss: 0.0271
Epoch 4700, Loss: 0.0268
Epoch 4800, Loss: 0.0265
Epoch 4900, Loss: 0.0261
Epoch 5000, Loss: 0.0295
Epoch 5100, Loss: 0.0256
Epoch 5200, Loss: 0.0253
Epoch 5300, Loss: 0.0254
Epoch 5400, Loss: 0.0247
Epoch 5500, Loss: 0.0247
Epoch 5600, Loss: 0.0254
Epoch 5700, Loss: 0.0239
Epoch 5800, Loss: 0.0236
Epoch 5900, Loss: 0.0234
Epoch 6000, Loss: 0.0232
Epoch 6100, Loss: 0.0229
Epoch 6200, Loss: 0.0227
Epoch 6300, Loss: 0.0225
Epoch 6400, Loss: 0.0225
Epoch 6500, Loss: 0.0220
Epoch 6600, Loss: 0.0219
Epoch 6700, Loss: 0.0216
Epoch 6800, Loss: 0.0215
Epoch 6900, Loss: 0.0212
Epoch 7000, Loss: 0.0228
Epoch 7100, Loss: 0.0210
Epoch 7200, Loss: 0.0208
Epoch 7300, Loss: 0.0207
Epoch 7400, Loss: 0.0205
Epoch 7500, Loss: 0.0204
Epoch 7600, Loss: 0.0203
Epoch 7700, Loss: 0.0201
Epoch 7800, Loss: 0.0200
Epoch 7900, Loss: 0.0198
Epoch 8000, Loss: 0.0197
Epoch 8100, Loss: 0.0196
Epoch 8200, Loss: 0.0194
Epoch 8300, Loss: 0.0194
Epoch 8400, Loss: 0.0193
Epoch 8500, Loss: 0.0189
Epoch 8600, Loss: 0.0189
Epoch 8700, Loss: 0.0186
Epoch 8800, Loss: 0.0185
Epoch 8900, Loss: 0.0183
Epoch 9000, Loss: 0.0182
Epoch 9100, Loss: 0.0181
Epoch 9200, Loss: 0.0179
Epoch 9300, Loss: 0.0177
Epoch 9400, Loss: 0.0176
Epoch 9500, Loss: 0.0174
Epoch 9600, Loss: 0.0173
Epoch 9700, Loss: 0.0172
Epoch 9800, Loss: 0.0172
Epoch 9900, Loss: 0.0174
Epoch 10000, Loss: 0.0167
Epoch 10100, Loss: 0.0166
Epoch 10200, Loss: 0.0170
Epoch 10300, Loss: 0.0164
Epoch 10400, Loss: 0.0162
Epoch 10500, Loss: 0.0166
Epoch 10600, Loss: 0.0160
Epoch 10700, Loss: 0.0159
Epoch 10800, Loss: 0.0158
Epoch 10900, Loss: 0.0157
Epoch 11000, Loss: 0.0156
Epoch 11100, Loss: 0.0156
Epoch 11200, Loss: 0.0161
Epoch 11300, Loss: 0.0156
Epoch 11400, Loss: 0.0156
Epoch 11500, Loss: 0.0157
Epoch 11600, Loss: 0.0155
Epoch 11700, Loss: 0.0172
Epoch 11800, Loss: 0.0155
Epoch 11900, Loss: 0.0155
Epoch 12000, Loss: 0.0155
Epoch 12100, Loss: 0.0155
Epoch 12200, Loss: 0.0155
Epoch 12300, Loss: 0.0155
Epoch 12400, Loss: 0.0155
Epoch 12500, Loss: 0.0155
Epoch 12600, Loss: 0.0155
Epoch 12700, Loss: 0.0156
Epoch 12800, Loss: 0.0155
Epoch 12900, Loss: 0.0156
Epoch 13000, Loss: 0.0155
Epoch 13100, Loss: 0.0155
Epoch 13200, Loss: 0.0155
Epoch 13300, Loss: 0.0155
Epoch 13400, Loss: 0.0155
Epoch 13500, Loss: 0.0156
Epoch 13600, Loss: 0.0155
Epoch 13700, Loss: 0.0155
Epoch 13800, Loss: 0.0155
Epoch 13900, Loss: 0.0155
Epoch 14000, Loss: 0.0155
Epoch 14100, Loss: 0.0155
Epoch 14200, Loss: 0.0155
Epoch 14300, Loss: 0.0155
Epoch 14400, Loss: 0.0155
Epoch 14500, Loss: 0.0155
Epoch 14600, Loss: 0.0155
Epoch 14700, Loss: 0.0155
Epoch 14800, Loss: 0.0155
Epoch 14900, Loss: 0.0157
Epoch 15000, Loss: 0.0158
Epoch 15100, Loss: 0.0155
Epoch 15200, Loss: 0.0155
Epoch 15300, Loss: 0.0155
Epoch 15400, Loss: 0.0155
Epoch 15500, Loss: 0.0155
Epoch 15600, Loss: 0.0155
Epoch 15700, Loss: 0.0155
Epoch 15800, Loss: 0.0155
Epoch 15900, Loss: 0.0155
Epoch 16000, Loss: 0.0155
Epoch 16100, Loss: 0.0155
Epoch 16200, Loss: 0.0156
Epoch 16300, Loss: 0.0169
Epoch 16400, Loss: 0.0155
Epoch 16500, Loss: 0.0155
Epoch 16600, Loss: 0.0155
Epoch 16700, Loss: 0.0155
Epoch 16800, Loss: 0.0155
Epoch 16900, Loss: 0.0155
Epoch 17000, Loss: 0.0155
Epoch 17100, Loss: 0.0156
Epoch 17200, Loss: 0.0155
Epoch 17300, Loss: 0.0155
Epoch 17400, Loss: 0.0155
Epoch 17500, Loss: 0.0155
Epoch 17600, Loss: 0.0155
Epoch 17700, Loss: 0.0158
Epoch 17800, Loss: 0.0155
Epoch 17900, Loss: 0.0155
Epoch 18000, Loss: 0.0155
Epoch 18100, Loss: 0.0155
Epoch 18200, Loss: 0.0155
Epoch 18300, Loss: 0.0157
Epoch 18400, Loss: 0.0155
Epoch 18500, Loss: 0.0155
Epoch 18600, Loss: 0.0156
Epoch 18700, Loss: 0.0155
Epoch 18800, Loss: 0.0160
Epoch 18900, Loss: 0.0155
Epoch 19000, Loss: 0.0155
Epoch 19100, Loss: 0.0155
Epoch 19200, Loss: 0.0155
Epoch 19300, Loss: 0.0155
Epoch 19400, Loss: 0.0155
Epoch 19500, Loss: 0.0155
Epoch 19600, Loss: 0.0155
Epoch 19700, Loss: 0.0156
Epoch 19800, Loss: 0.0156
Epoch 19900, Loss: 0.0155
Epoch 20000, Loss: 0.0155
Epoch 20100, Loss: 0.0156
Epoch 20200, Loss: 0.0155
Epoch 20300, Loss: 0.0170
Epoch 20400, Loss: 0.0156
Epoch 20500, Loss: 0.0155
Epoch 20600, Loss: 0.0155
Epoch 20700, Loss: 0.0155
Epoch 20800, Loss: 0.0158
Epoch 20900, Loss: 0.0155
Epoch 21000, Loss: 0.0155
Epoch 21100, Loss: 0.0155
Epoch 21200, Loss: 0.0156
Epoch 21300, Loss: 0.0155
Epoch 21400, Loss: 0.0155
Epoch 21500, Loss: 0.0155
Epoch 21600, Loss: 0.0155
Epoch 21700, Loss: 0.0175
Epoch 21800, Loss: 0.0155
Epoch 21900, Loss: 0.0155
Epoch 22000, Loss: 0.0155
Epoch 22100, Loss: 0.0156
Epoch 22200, Loss: 0.0155
Epoch 22300, Loss: 0.0157
Epoch 22400, Loss: 0.0155
Epoch 22500, Loss: 0.0155
Epoch 22600, Loss: 0.0155
Epoch 22700, Loss: 0.0155
Epoch 22800, Loss: 0.0155
Epoch 22900, Loss: 0.0230
Epoch 23000, Loss: 0.0155
Epoch 23100, Loss: 0.0155
Epoch 23200, Loss: 0.0155
Epoch 23300, Loss: 0.0155
Epoch 23400, Loss: 0.0155
Epoch 23500, Loss: 0.0155
Epoch 23600, Loss: 0.0155
Epoch 23700, Loss: 0.0155
Epoch 23800, Loss: 0.0164
Epoch 23900, Loss: 0.0155
Epoch 24000, Loss: 0.0155
Epoch 24100, Loss: 0.0155
Epoch 24200, Loss: 0.0155
Epoch 24300, Loss: 0.0155
Epoch 24400, Loss: 0.0155
Epoch 24500, Loss: 0.0155
Epoch 24600, Loss: 0.0155
Epoch 24700, Loss: 0.0158
Epoch 24800, Loss: 0.0155
Epoch 24900, Loss: 0.0155
Epoch 25000, Loss: 0.0161
Epoch 25100, Loss: 0.0155
Epoch 25200, Loss: 0.0155
Epoch 25300, Loss: 0.0157
Epoch 25400, Loss: 0.0155
Epoch 25500, Loss: 0.0155
Epoch 25600, Loss: 0.0155
Epoch 25700, Loss: 0.0155
Epoch 25800, Loss: 0.0155
Epoch 25900, Loss: 0.0155
Epoch 26000, Loss: 0.0156
Epoch 26100, Loss: 0.0155
Epoch 26200, Loss: 0.0155
Epoch 26300, Loss: 0.0155
Epoch 26400, Loss: 0.0155
Epoch 26500, Loss: 0.0155
Epoch 26600, Loss: 0.0155
Epoch 26700, Loss: 0.0155
Epoch 26800, Loss: 0.0155
Epoch 26900, Loss: 0.0155
Epoch 27000, Loss: 0.0155
Epoch 27100, Loss: 0.0155
Epoch 27200, Loss: 0.0155
Epoch 27300, Loss: 0.0155
Epoch 27400, Loss: 0.0155
Epoch 27500, Loss: 0.0159
Epoch 27600, Loss: 0.0155
Epoch 27700, Loss: 0.0155
Epoch 27800, Loss: 0.0155
Epoch 27900, Loss: 0.0155
Epoch 28000, Loss: 0.0155
Epoch 28100, Loss: 0.0155
Epoch 28200, Loss: 0.0155
Epoch 28300, Loss: 0.0155
Epoch 28400, Loss: 0.0155
Epoch 28500, Loss: 0.0155
Epoch 28600, Loss: 0.0155
Epoch 28700, Loss: 0.0155
Epoch 28800, Loss: 0.0155
Epoch 28900, Loss: 0.0159
Epoch 29000, Loss: 0.0155
Epoch 29100, Loss: 0.0155
Epoch 29200, Loss: 0.0259
Epoch 29300, Loss: 0.0155
Epoch 29400, Loss: 0.0155
Epoch 29500, Loss: 0.0155
Epoch 29600, Loss: 0.0155
Epoch 29700, Loss: 0.0155
Epoch 29800, Loss: 0.0155
Epoch 29900, Loss: 0.0155

nn_fits = md_nn(x_torch).detach().numpy()
plt.figure(figsize = (12, 6))
plt.plot(x_scaled, y_scaled, color = 'blue', label = 'Data')
#plt.plot(x_scaled, md_c2.fittedvalues, color = 'black', label = 'Fitted Values')
plt.plot(x_scaled, nn_fits, color = 'red', label = 'PyTorch Fitted Values')
plt.legend()
plt.show()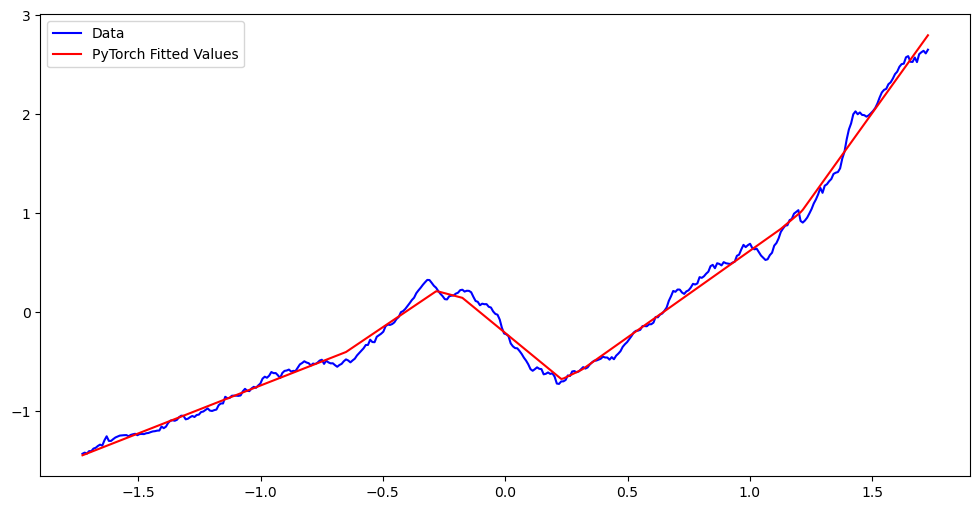
<Figure size 1200x600 with 1 Axes>

AutoRegression

Next we fit the NonLinear AR(1) model. We will generate a simulated dataset using the following equation:

yt=2yt−11+0.8yt−12+ϵty_t = \frac{2 y_{t-1}}{1 + 0.8 y_{t-1}^2} + \epsilon_t

where ϵt∼i.i.duniform(−1,1)\epsilon_t \overset{\text{i.i.d}}{\sim} \text{uniform}(-1, 1).

n = 195
#n = 240
rng = np.random.default_rng(seed = 40)
eps = rng.uniform(low = -1.0, high = 1.0, size = n) 
#sig = 1.0
#eps = rng.normal(loc = 0.0, scale = sig, size = n)

y_sim = np.full(n, 0, dtype = float) 
for i in range(1, n):
    y_sim[i] = ((2*y_sim[i-1])/(1 + 0.8 * (y_sim[i-1] ** 2))) + eps[i]

plt.figure(figsize = (12, 6))
plt.plot(y_sim)
plt.show()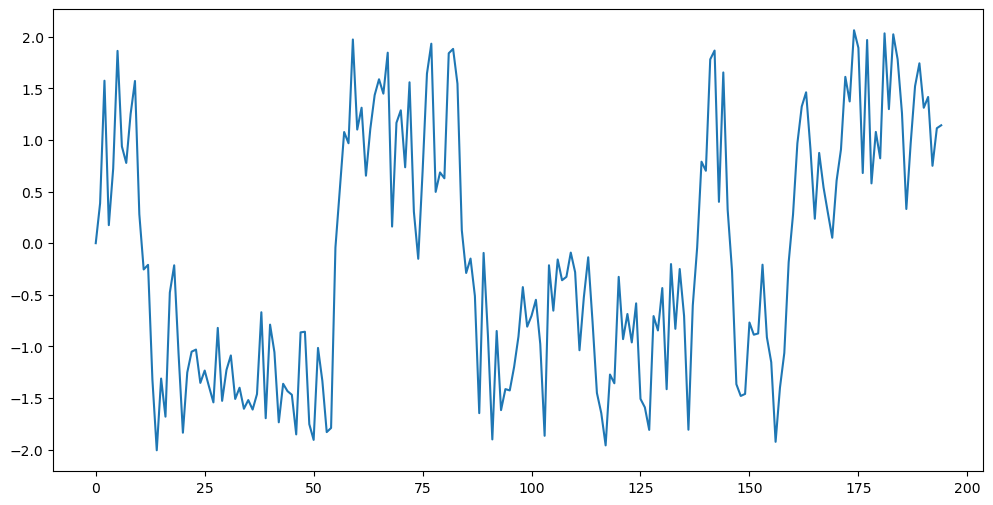
<Figure size 1200x600 with 1 Axes>

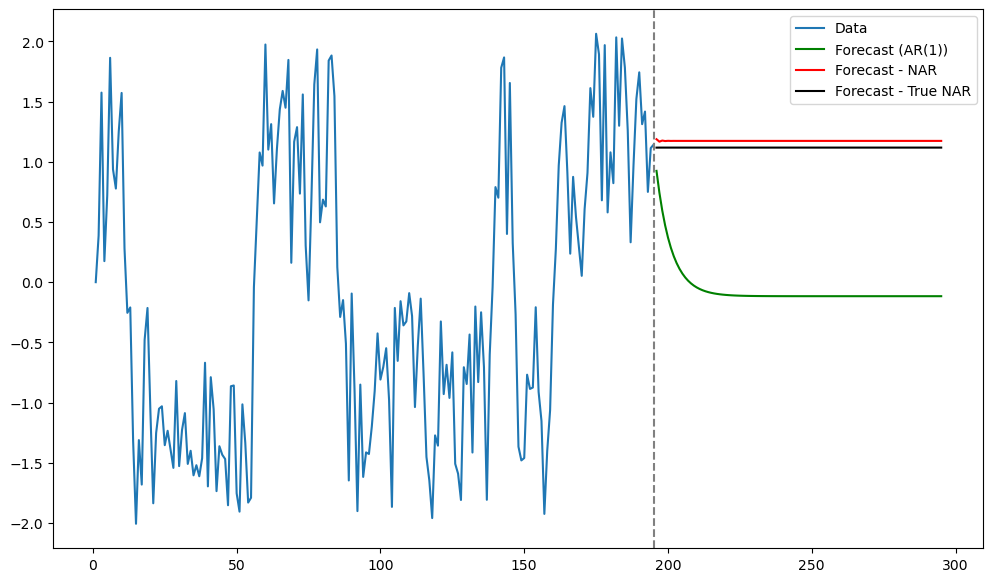
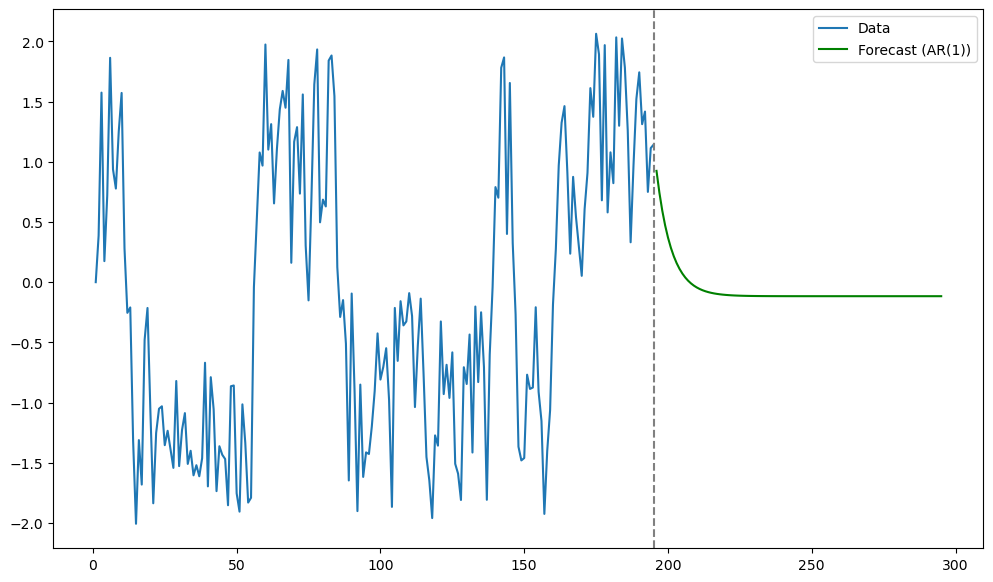
Looking at the dataset, it is natural to predict the next values at around level 1. The usual linear AR(1) model predicts closer to the overall mean which is not ideal in this situation. In contrast, the nonlinear AR(1) model obtains predictions that match with intuition.

The function g(⋅)g(\cdot) which generated the data yt=g(yt−1)+ϵty_t = g(y_{t-1}) + \epsilon_t is plotted below.

def g(x):
    return 2 * x / (1 + 0.8 * x**2)

x_vals = np.linspace(-2, 2, 400)
y_vals = g(x_vals)

# Plot the function
plt.figure(figsize = (12, 6))
plt.plot(x_vals, y_vals)
plt.title(r'$g(x) = \frac{2x}{1 + 0.8x^2}$')
plt.xlabel('x')
plt.ylabel('g(x)')
plt.grid(True)
plt.show()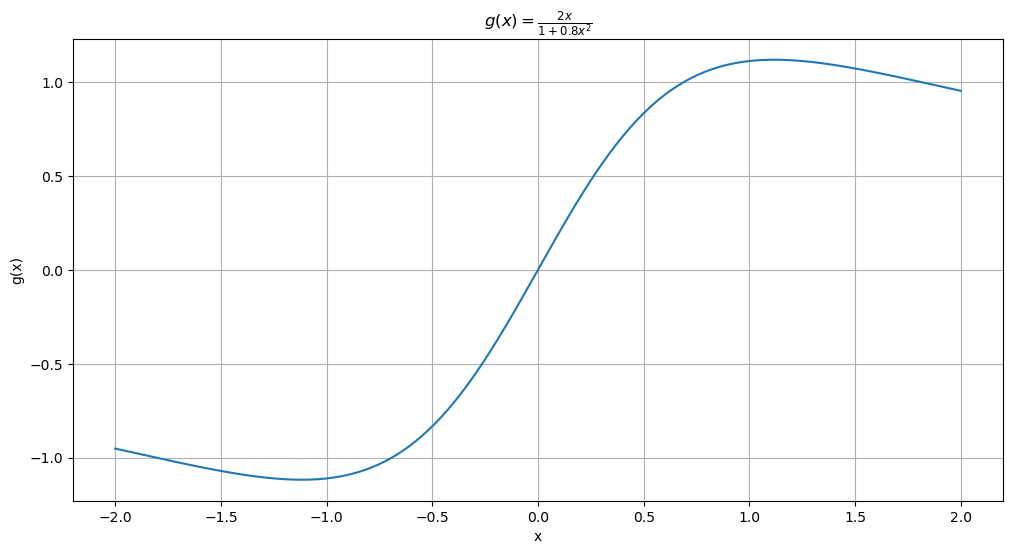
<Figure size 1200x600 with 1 Axes>

Let us first fit the usual AR(1) model, and look at the predictions.

ar = ARIMA(y_sim, order = (1, 0, 0)).fit()
print(ar.summary())
n_y = len(y_sim)
tme = range(1, n_y+1)
k_future = 100 #number of future points for prediction
tme_future = range(n_y+1, n_y+k_future+1)
fcast = ar.get_prediction(start = n_y, end = n_y+k_future-1).predicted_mean
plt.figure(figsize = (12, 7))
plt.plot(tme, y_sim, label = 'Data')
plt.plot(tme_future, fcast, label = 'Forecast (AR(1))', color = 'green')
plt.axvline(x=n_y, color='gray', linestyle='--')
plt.legend()
plt.show()
                               SARIMAX Results                                
==============================================================================
Dep. Variable:                      y   No. Observations:                  195
Model:                 ARIMA(1, 0, 0)   Log Likelihood                -197.447
Date:                Fri, 25 Apr 2025   AIC                            400.893
Time:                        18:50:36   BIC                            410.712
Sample:                             0   HQIC                           404.869
                                - 195                                         
Covariance Type:                  opg                                         
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
const         -0.1165      0.277     -0.420      0.675      -0.660       0.427
ar.L1          0.8268      0.041     20.335      0.000       0.747       0.906
sigma2         0.4410      0.056      7.826      0.000       0.331       0.551
===================================================================================
Ljung-Box (L1) (Q):                   5.47   Jarque-Bera (JB):                 4.50
Prob(Q):                              0.02   Prob(JB):                         0.11
Heteroskedasticity (H):               1.15   Skew:                             0.11
Prob(H) (two-sided):                  0.57   Kurtosis:                         2.29
===================================================================================

Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
<Figure size 1200x700 with 1 Axes>

Next we will fit the nonlinear AR(1) model using PyTorch.

class PiecewiseLinearModel(nn.Module):
    def __init__(self, knots_init, beta_init):
        super().__init__()
        self.num_knots = len(knots_init)
        self.beta = nn.Parameter(torch.tensor(beta_init, dtype=torch.float32)) 
        self.knots = nn.Parameter(torch.tensor(knots_init, dtype=torch.float32))

    def forward(self, x):
        knots_sorted, _ = torch.sort(self.knots)
        out = self.beta[0] + self.beta[1] * x
        for j in range(self.num_knots):
            out += self.beta[j + 2] * torch.relu(x - knots_sorted[j])
        return out
y_reg = y_sim[1:]
x_reg = y_sim[0:(n-1)]

y_torch = torch.tensor(y_reg, dtype = torch.float32).unsqueeze(1)
x_torch = torch.tensor(x_reg, dtype = torch.float32).unsqueeze(1)
k = 6
quantile_levels = np.linspace(1/(k+1), k/(k+1), k)
knots_init = np.quantile(x_reg, quantile_levels)

n_reg = len(y_reg)
X = np.column_stack([np.ones(n_reg), x_reg])
for j in range(k):
    xc = ((x_reg > knots_init[j]).astype(float))*(x_reg - knots_init[j])  
    X = np.column_stack([X, xc])
md_init = sm.OLS(y_reg, X).fit()
beta_init = md_init.params
print(knots_init)
print(beta_init)
[-1.47418868 -1.05574615 -0.65832485 -0.09346269  0.70088161  1.39251632]
[-2.48088937 -0.77905517  1.14589238  0.11575653  0.79468018  0.80873226
 -2.52554882  0.48737735]

nar = PiecewiseLinearModel(knots_init = knots_init, beta_init = beta_init)
optimizer = optim.Adam(nar.parameters(), lr = 0.01)
loss_fn = nn.MSELoss()

for epoch in range(10000): 
    optimizer.zero_grad()
    y_pred = nar(x_torch)
    loss = loss_fn(y_pred, y_torch)
    loss.backward()
    optimizer.step()
    if epoch % 100 == 0: 
        print(f"Epoch {epoch}, Loss: {loss.item():.4f}")
#Run this code a few times to be sure of convergence. 
Epoch 0, Loss: 0.3025
Epoch 100, Loss: 0.2982
Epoch 200, Loss: 0.2980
Epoch 300, Loss: 0.2979
Epoch 400, Loss: 0.2978
Epoch 500, Loss: 0.2977
Epoch 600, Loss: 0.2976
Epoch 700, Loss: 0.2976
Epoch 800, Loss: 0.2975
Epoch 900, Loss: 0.2975
Epoch 1000, Loss: 0.2974
Epoch 1100, Loss: 0.2974
Epoch 1200, Loss: 0.2974
Epoch 1300, Loss: 0.2973
Epoch 1400, Loss: 0.2973
Epoch 1500, Loss: 0.2973
Epoch 1600, Loss: 0.2972
Epoch 1700, Loss: 0.2972
Epoch 1800, Loss: 0.2972
Epoch 1900, Loss: 0.2972
Epoch 2000, Loss: 0.2972
Epoch 2100, Loss: 0.2972
Epoch 2200, Loss: 0.2971
Epoch 2300, Loss: 0.2971
Epoch 2400, Loss: 0.2971
Epoch 2500, Loss: 0.2971
Epoch 2600, Loss: 0.2971
Epoch 2700, Loss: 0.2971
Epoch 2800, Loss: 0.2971
Epoch 2900, Loss: 0.2971
Epoch 3000, Loss: 0.2971
Epoch 3100, Loss: 0.2971
Epoch 3200, Loss: 0.2971
Epoch 3300, Loss: 0.2971
Epoch 3400, Loss: 0.2971
Epoch 3500, Loss: 0.2971
Epoch 3600, Loss: 0.2971
Epoch 3700, Loss: 0.2971
Epoch 3800, Loss: 0.2971
Epoch 3900, Loss: 0.2971
Epoch 4000, Loss: 0.2971
Epoch 4100, Loss: 0.2971
Epoch 4200, Loss: 0.2971
Epoch 4300, Loss: 0.2971
Epoch 4400, Loss: 0.2971
Epoch 4500, Loss: 0.2971
Epoch 4600, Loss: 0.2971
Epoch 4700, Loss: 0.2971
Epoch 4800, Loss: 0.2971
Epoch 4900, Loss: 0.2971
Epoch 5000, Loss: 0.2971
Epoch 5100, Loss: 0.2971
Epoch 5200, Loss: 0.2971
Epoch 5300, Loss: 0.2971
Epoch 5400, Loss: 0.2971
Epoch 5500, Loss: 0.2971
Epoch 5600, Loss: 0.2971
Epoch 5700, Loss: 0.2971
Epoch 5800, Loss: 0.2971
Epoch 5900, Loss: 0.2971
Epoch 6000, Loss: 0.2971
Epoch 6100, Loss: 0.2971
Epoch 6200, Loss: 0.2971
Epoch 6300, Loss: 0.2971
Epoch 6400, Loss: 0.2971
Epoch 6500, Loss: 0.2971
Epoch 6600, Loss: 0.2971
Epoch 6700, Loss: 0.2971
Epoch 6800, Loss: 0.2971
Epoch 6900, Loss: 0.2971
Epoch 7000, Loss: 0.2971
Epoch 7100, Loss: 0.2971
Epoch 7200, Loss: 0.2971
Epoch 7300, Loss: 0.2971
Epoch 7400, Loss: 0.2971
Epoch 7500, Loss: 0.2971
Epoch 7600, Loss: 0.2971
Epoch 7700, Loss: 0.2971
Epoch 7800, Loss: 0.2971
Epoch 7900, Loss: 0.2971
Epoch 8000, Loss: 0.2971
Epoch 8100, Loss: 0.2971
Epoch 8200, Loss: 0.2971
Epoch 8300, Loss: 0.2971
Epoch 8400, Loss: 0.2971
Epoch 8500, Loss: 0.2971
Epoch 8600, Loss: 0.2971
Epoch 8700, Loss: 0.2971
Epoch 8800, Loss: 0.2971
Epoch 8900, Loss: 0.2971
Epoch 9000, Loss: 0.2971
Epoch 9100, Loss: 0.2971
Epoch 9200, Loss: 0.2971
Epoch 9300, Loss: 0.2971
Epoch 9400, Loss: 0.2971
Epoch 9500, Loss: 0.2971
Epoch 9600, Loss: 0.2971
Epoch 9700, Loss: 0.2971
Epoch 9800, Loss: 0.2971
Epoch 9900, Loss: 0.2971

Below we compute the predictions given by the nonlinear AR model.

last_val = torch.tensor([[y_sim[-1]]], dtype = torch.float32)
future_preds = []
for _ in range(k_future):
    next_val = nar(last_val)
    future_preds.append(next_val.item())
    last_val = next_val.detach()
future_preds_array = np.array(future_preds)

We also compute predictions using the actual function gg which generated the data.

last_val = torch.tensor([[y_sim[-1]]], dtype = torch.float32)
actual_preds = []
for _ in range(k_future):
    next_val = ((2*last_val)/(1 + 0.8 * (last_val ** 2)))
    actual_preds.append(next_val.item())
    last_val = next_val.detach()
actual_preds_array = np.array(actual_preds)

n_y = len(y_sim)
tme = range(1, n_y+1)
tme_future = range(n_y+1, n_y+k_future+1)
fcast = ar.get_prediction(start = n_y, end = n_y+k_future-1).predicted_mean
plt.figure(figsize = (12, 7))
plt.plot(tme, y_sim, label = 'Data')
plt.plot(tme_future, fcast, label = 'Forecast (AR(1))', color = 'green')
plt.plot(tme_future, future_preds_array, label = 'Forecast - NAR', color = 'red')
plt.plot(tme_future, actual_preds_array, label = 'Forecast - True NAR', color = 'black')
plt.axvline(x=n_y, color='gray', linestyle='--')
plt.legend()
plt.show()
<Figure size 1200x700 with 1 Axes>
Stat 153
Stationary solutions, Box-Jenkins Modeling, AIC and BIC
Stat 153
Fitting Change of Slope Models via Pytorch: importance of scaling